TP3 : Vectorisation, Logiques et Broadcasting

Extraction d'éléments d'un tableau

1. Créer une matrice A de dimensions 6x5, d'entiers tirés aléatoirement entre 2 et 15. Afficher A
2. Extraire de la matrice A, la sous matrice 3x3 en ne récupérant que les éléments "en bas" et "à droite".
3. Faire une matrice B à partir de la matrice A qui contient une ligne sur deux et une colonne sur deux de A en partant de la première ligne et de la première colonne.

# Réponse 

Création de matrices

1. Créer une matrice C (6x4) remplie avec la valeur 5.5
2. Faire compter le nombre d'éléments de C
3. Redimensionner la matrice C pour que ses nouvelles dimensions soient (3x8)
4. Faire afficher le nombre de colonnes de C et le nombre de lignes
5. Créer une matrice carrée D ayant sur sa diagonale les nombres impairs de 1 à 9 inclus.L'afficher

# Réponse 

Manipulations de matrices

A chaque étape, il est conseillé de vérifier ce que vous obtenez avec l'explorateur de variables ou en faisant des print().

1. Créer un vecteur vpair de 4 nombres consécutifs pairs en partant de 2.
2. Créer un vecteur vimpair de 5 nombres consécutifs impairs en partant de 1.
3. Transformer le vecteur vpair en un vecteur colonne (4,1) avec np.newaxis
4. Transformer le vecteur vimpair en un vecteur ligne (1,5) avec np.newaxis
5. Faire une matrice VS qui est la somme de vpair et vimpair
6. Créer VSrot en faisant deux rotations à 90 de VS
7. Avec np.flipud, "Retourner" et écraser VS pour inverser l'ordre des lignes.
8. Avec np.fliplr, "Retourner" et écraser VS obtenu ci dessus pour inverser l'ordre des colonnes
9. Soustraire VS à VSrot, afficher le résultat

Indices : utilisation de np.rot90, np.fliplr, np.flipud

# Réponse 

Opérations avec des logiques

Etant donné $x=\begin{bmatrix} 3&15&9&-12&-1&0&12&9&6&1\end{bmatrix} $, écrire la commande ($\textbf{une seule instruction !}$) qui permet de réaliser les fonctionnalités suivantes: (dans votre script, si le vecteur x est modifié par la commande, il faut le réinitialiser à sa valeur de départ avant de faire la commande suivante)

Exemple : Mise à zéro des valeurs de x positives ou nulles, les autres valeurs sont conservées ;

1. Mise à la valeur 3 des valeurs de x qui sont des multiples de 3, les autres valeurs sont conservées ;
2. Multiplication des valeurs paires par 5, les autres valeurs sont conservées ;
3. Extraction des valeurs de x qui sont supérieures ou égales à 10 pour les placer dans un vecteur y ;
4. Mettre à la valeur moyenne du vecteur x, toutes les valeurs de x qui sont strictement inférieures à cette moyenne, les autres valeurs sont conservées
5. Remplacer les valeurs de x strictement supérieures à la valeur moyenne du vecteur x, par la différence avec cette moyenne, les autres valeurs sont conservées.
6. Faire afficher le nombre de valeurs négatives dans x.

Le fonctions de numpy np.mod (ou %) et np.mean peuvent être utiles.

# Exemple
xorig = np.array([3.0,15,9,-12,-1,0,12,9,6,1])
print(xorig)
x = xorig.copy() # On copie xorig en x
x[x>=0]=0
print(x)

# Réponse 

Graphiques : répétitions de motifs

• Écrire des scripts qui reproduisent approximativement les graphiques suivants :

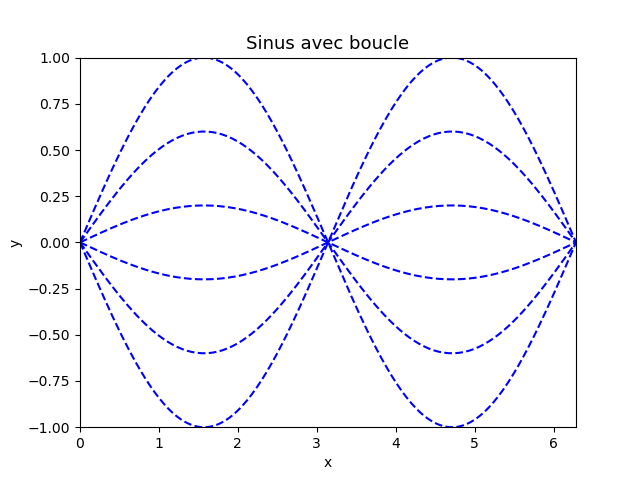
Faire deux versions : une avec boucle et l'autre sans boucle

import matplotlib.pyplot as plt

# SINUS
x = np.linspace(0,2*np.pi,200)

# Version avec boucle
# Réponse 

# Version sans boucle

# Réponse 

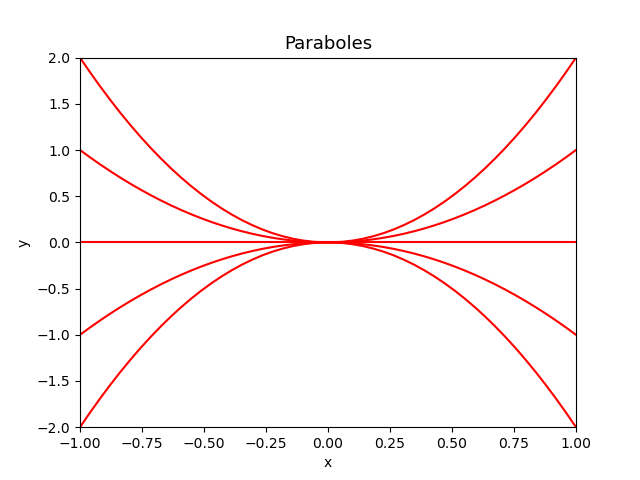
A faire sans boucle

# Réponse 

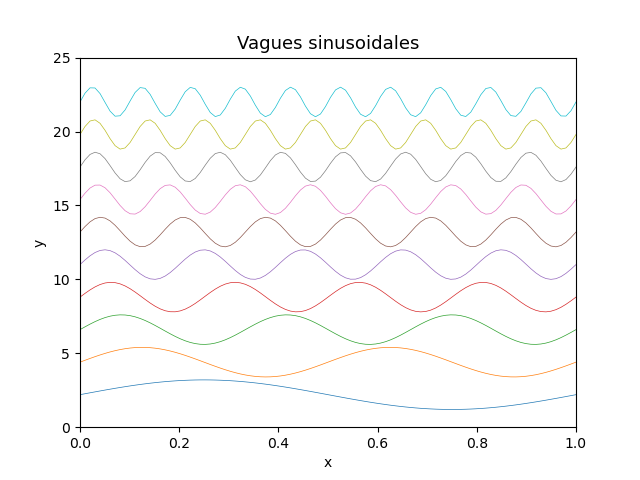
A faire sans boucle

# Réponse 

Suites et séries : vectorisation

La fonction np.cumsum sera utile dans les questions suivantes.

Constante d'Euler

La constante d'Euler e est la valeur de la fonction exponentielle $e^x$ avec $x=1$. Le développement en série de la fonction exponentielle s'écrit :

\begin{equation*} e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \dots + \frac{x^n}{n!} + \dots \end{equation*}

On définit la série $e_N(x)$ par:

$$ e_N(x) = \sum_{n=0}^N \frac{x^n}{n!} $$

de sorte que $e^x = \lim_{N \to +\infty} e_N(x)$

1. En retenant 10 termes de la série, calculer une approximation de la constante d’Euler.
2. Tracer en échelle semilogy l'écart en valeur absolue à $|e - e_N(1)|$ en fonction du nombre de termes retenus, N allant de 1 à 10.

Vous devriez obtenir la figure suivante :

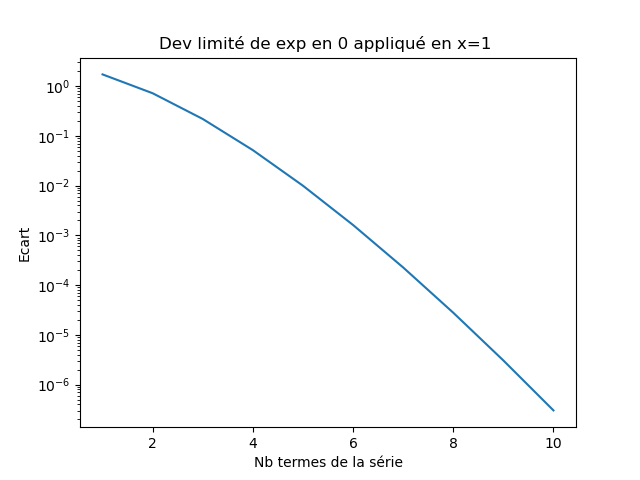
# EXERCICE CONVERGENCE DE LA SERIE DE e

from scipy.special import factorial

# Réponse 

Series pour Ln et Sinus

Dans le même esprit que pour le calcul de la constante d'Euler, pour les deux series programmées avec des boucles lors du TP2 (ln(x) et sin(x)), programmez les à nouveau mais sans utiliser de boucles et en utilsant le broadcasting. Refaites aussi les trois graphes demandés au TP2.

# SERIE LN(X)

# Réponse 

# SERIE SIN(X)

# Réponse