TP 2 : Approfondissement de Python : Séries, Fichiers (lecture/écriture) et Courbes paramétrées.¶

Série de fonctions¶

Pour tout $x \in , ]0;+\infty[$, un développement en série à l'ordre N de la fonction ln(x) est donné par : $$ ln_N(x) = \sum_{n=0}^{N} \frac{2}{2n+1}\left(\frac{x-1}{x+1}\right)^ {2n+1} $$

En faisant varier $N$ de 0 à 100, calculer la valeur du développement pour $x=80$ et la valeur de l'erreur $E_N(80) = (ln_N(80) - ln(80))^2$.
Lors du calcul du développement et de l'erreur, vous allez stocker les valeurs dans un tableau afin de reproduire la figure ci-dessous:

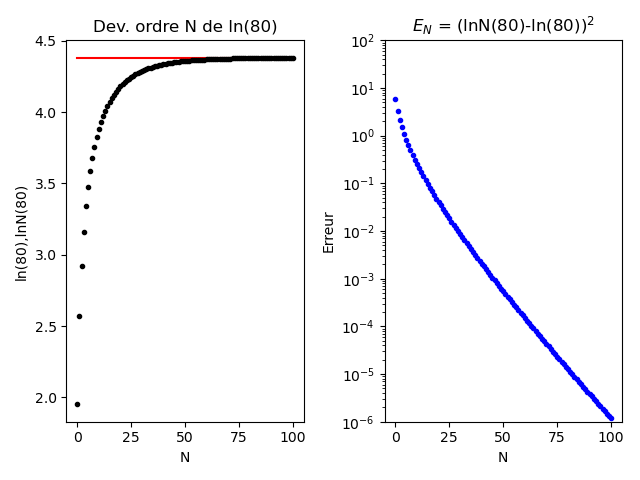
Prendre soin de mettre les titres, les noms des axes, d'utiliser subplot. Utiliser aussi la fonction str et une variable pour éviter les répétitions de code et saisir 80 plusieurs fois dans les titres ou labels des figures.

In [ ]:

# Réponse

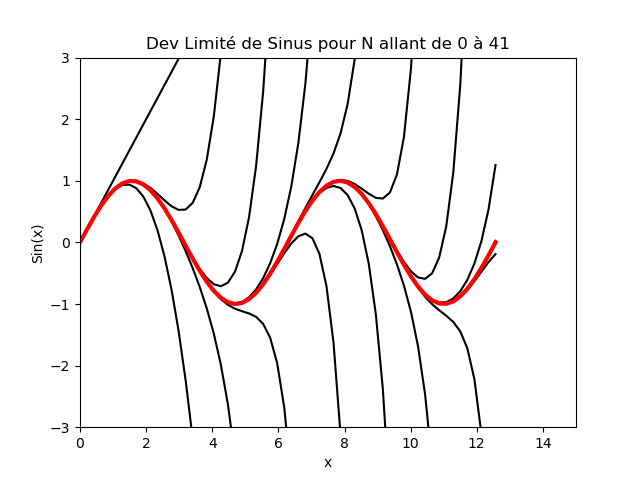
Pour x réel, on donne le développement en série à l'ordre N de la fonction sin(x) : $$ \sin_N(x) = \sum_{n=0}^N \frac{(-1)^n}{(2n+1)!} x^{2n+1} $$ Pour $x \in [0,4\pi]$,

Pour différentes valeurs de N allant de 0 à 40, tracer en noir sur une même figure le développment tronqué à N.
Superposer la courbe exacte sinus en rouge en trait plus épais comme le montre la figure ci-dessous (se servir de ylim).

In [ ]:

# On importe la fonction factorielle de la bibiothèque scipy.special avec from 
# une fois importée avec from son utilisation est très directe : factorial(n)

from scipy.special import factorial

print("Factoriel de 5 = ",factorial(5))

# Réponse

Lecture / Ecriture de fichier avec python et numpy¶

Dans cette première partie, on se propose de manipuler la lecture et l'ouverture de fichier avec python. Pour manipuler ces notions, on étudie la chute d'une balle de masse $m = 0.1 kg$ se situant à une hauteur $H=1 m$ de l'origine et se déplaçant avec une vitesse initiale $\overrightarrow{v}_b(t=0) = 0.15 \overrightarrow{e}_x$. On néglige les frottements de l'air et on considère la balle comme un point matériel. Son équation du mouvement est donc:

$\frac{d^2}{dt^2} \overrightarrow{x}_b (t) = \overrightarrow{g}$

Sa solution analytique: $x_b(t) = 0.15 t \\ $ $y_b(t) = - \frac{g*t^2}{2} + H$

On propose alors d'écrire les coordonnées $x_b$,$y_b$ de la balle au cours du temps dans un fichier compte tenu de la solution analytique donnée :

Créer un tableau numpy contenant le temps t allant de 0 à 1 s (le choix du pas est libre).
Calculer les coordonnées du vecteur position de la balle $x_b$,$y_b$.
Représenter $y_b$ au cours du temps.
En observant cette courbe, déterminer l'intervalle de temps (en secondes) où la balle atteint le sol. Faire afficher votre réponse (avec print). La précision sur les bornes de l'intervalle sera de un chiffre significatif.
Avec une résolution analytique, trouver le temps en fonction de $g$ et $H$. Faire afficher la valeur analytique.
Ecrire sur trois colonnes le temps, les coordonnées $x_b$,$y_b$ dans un fichier nommé "position.dat"

In [ ]:

# Réponse

On se propose maintenant de représenter sur un graphique les différentes énergies du système (balle). L'énergie potentielle et mécanique préalablement calculées se trouvent dans le fichier "energy.dat":

La première colonne correspond au temps
La deuxième colonne correspond à l'énergie potentielle
La troisième colonne correspond à l'énergie cinétique (ATTENTION : Il y a un délimiteur)

A partir des énergies potentielle et cinétique :

Lire le fichier "energy.dat" afin d'obtenir le temps, l'énergie cinétique et l'énergie potentielle dans trois tableaux numpy.
Calculez l'énergie mécanique
Tracez sur une même figure les courbes de l'évolution au cours du temps de l'énergie potentielle, l'énergie cinétique et l'énergie mécanique. Mettre une légende et les labels aux axes.
Faire écrire par votre script (avec un print) une phrase de conclusion.

In [ ]:

# Réponse

Courbes paramétrées¶

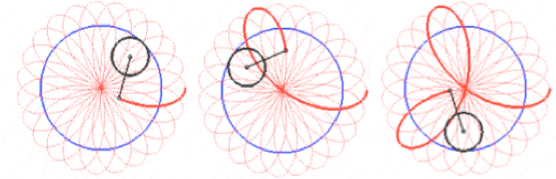
Les hypotrochoïdes sont des courbes décrites par un point lié à un disque roulant sans glisser intérieurement à un cercle de base. Ce sont des courbes que l’on obtient avec un spirographe avec disque interne. Ce qui nous intéresse dans cette partie du TP, c’est que bien que la formule mathématique soit toujours la même, la forme des courbes peut changer beaucoup lorsque l’on fait varier les paramètres qui la définissent. Nous allons nous intéresser aux rosaces qui sont des cas particuliers d’hypotrochoïde.

La représentation cartésienne des rosaces est définie par x=rcos(θ), y =rsin(θ), avec la définition du rapport entre le rayon et l’angle : r=cos(nθ) où n est le seul paramètre. Saurez-vous reproduire la figure suivante, qui représente une série de rosaces pour n=1,2,3,4,5, n=1/2,3/2,5/2,7/2,9/2 et n=1/3,2/3,4/3,5/3,7/3 ?

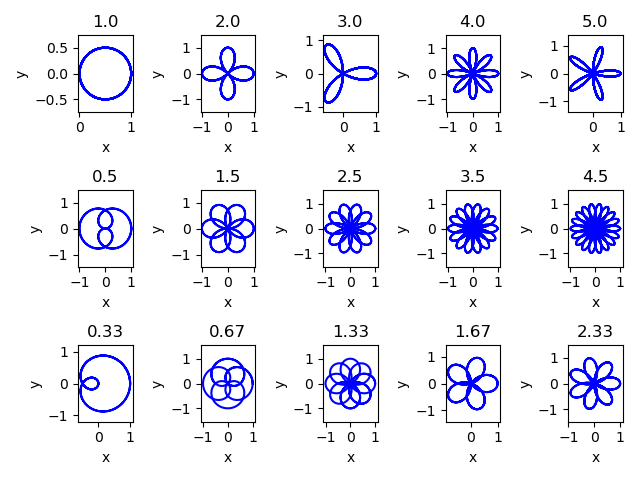
Indications : Choisir un intervalle pour $\theta$ qui permet de reproduire toutes les figures. Faire un grand vecteur contenant toutes les valeurs de n. Utiliser une boucle qui parcourt ce vecteur et trace les rosaces dans chaque case d'un tableau nblig x nbcol = 3 x 5 de sous-figures à l'aide de subplot(nblig,nbcol, ? )

In [ ]:

# Réponse