TP 1 : Prise en main de Python

Dans un premier temps, vous allez utiliser Python de manière interactive dans la console de spyder.

Calculatrice et manipulations simples de listes

• Créez une variable a dans laquelle vous mettez 5
• Executez la commande b = a + 0.0
• Quel est le type des variables a et b ?
• Quel est le résultat de a + b ?
• Quel est le résultat de 'a' + 'b' ?
• Quel est le résultat de 3*'a' ,
• Créez une liste nommée c qui contient les éléments suivant : 1, "Bonjour", 5.5, 8
• Affichez l'élément 5.5 de la liste c
• Remplacez dans la liste c la valeur 5.5 par "Bonsoir" et vérifiez que cela fonctionne en affichant cette liste
• Insérez le complexe 1+6i en deuxième position de la liste après 1 et avant 'Bonjour'.
• Supprimer l'avant dernier élément de cette liste.
• Ajoutez en bout de liste le réel 5.6

# Réponse 

Quelques opérateurs mathématiques et conversions de types

Les opérateurs // et % sont les quotients et le reste de la division entière. $**$ est la puissance. Les autres opérateurs sont classiques +,-,*,/.

Observez ce qui se passe quand vous tapez

• 20//3
• 20%3
• 2**4

Il est possible de convertir des données d'un type dans un autre, observez ce qui se passe pour

• int(3.0)
• int(3.7)
• float(3)
• str(4.4)
• int("3")
• float("3.5")
• int("3.5")
• int("Hello")

# Réponse 

Messages d'erreur

Pour les commandes suivantes, essayez d'interpréter les messages d'erreur.

• 8/0
• 20@4
• "hello"/3
• (3+2))*6

# Réponse 

Utilisation de bibliothèques

Importer les deux bibliothèques math et cmath avec les commandes:

• import math

• import cmath

• Calculez la valeur de $\cos( \pi /4)$

• Que vaut $\sqrt{-1}$ avec la bibliothèque math et avec la bibliothèque cmath ?

• Peut on calculer la racine carrée ou le cosinus d'une liste ? Essayez math.sqrt([2,3,4]) ou math.cos([math.pi/3, math.pi/2])

# Réponse 

Séquences d'entiers

A l'aide de la commande, list(range( )), il faut générer les séquences d'entiers suivantes:

• [-10, -3, 4]
• [-10, -13, -16, -19]
• [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
• [-1, 2, 5, 8, 11]

# Réponse 

Premier script

En vous servant de spyder, vous allez faire votre premier script.

Première boucle et premier test.

Dans le script

• Faire une boucle qui calcule et affiche les cubes $i^3$ pour $i$ allant de 1 à 10.
• Faire la même opération mais en affichant avec un test seulement les cas où $i$ est pair.

Sauvegardez le script Prise_en_main.py dans un répertoire par exemple TP1.Bien repérer où se trouve le fichier, créez des répertoires ou sous répertoires bien identifiés sur le disque dur.

# Réponse 

Utilisation basique de Numpy

Importer numpy avec la commande import numpy as np.

• Faire avec np.linspace() un tableau a des floats allant de 0.0 à 3.2 inclus avec 9 valeurs
• Faire le même tableau appelé b avec np.arange().
• Mettre toutes les valeurs du tableau b au carré et les afficher
• Prendre la raciné carrée de toutes les valeurs de a et les afficher

# Réponse 

Les graphiques

Importer matplotlib avec la commande import matplotlib.pyplot as plt

Comprendre ce que font les commandes suivantes :

• plt.plot([0,2,1,0,0], [0,0,1.5,1,0])
• plt.axis([-1,2.5,-2,3])

# Réponse 

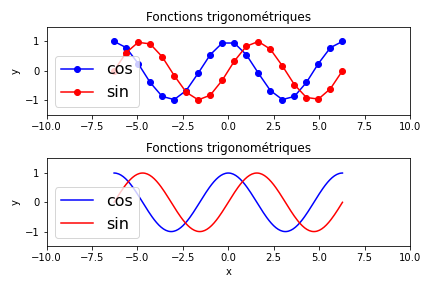
Courbes trigonométriques

En utilisant subplot pour créer deux sous-graphiques dans la même figure

• Tracer un cosinus avec 20 points en abscisse (bien observer les valeurs des abscisses et utiliser la fonction linspace de numpy)
• Faire la même chose avec 200 points pour le deuxième graphique.
• Ajouter dans chaque sous-graphique une courbe sinus.
• Indiquer le nom des axes.
• Mettre des titres, des légendes.
• Redéfinir les limites des axes.

Vous devez obtenir la figure suivante:

# Réponse 

Graphiques avec des boucles :

• Tracez un triangle équilatéral en choisissant les coordonnées des points à donner à la fonction plt.plot.
• A l'aide d'une boucle for tracez 10 triangles en changeant leur position de 0.15 en x et y et leur taille en grossissant de 1.05.
• Les deux graphiques seront mis cote à cote à l'aide de plt.subplot().

Vous devez obtenir la figure suivante : (pour mettre les axes à la même échelle, on utilise plt.axis('equal'))

Remarque : Comme le triangle est équilatéral, les coordonnées du sommet ne sont pas (0.5,1) !

# Réponse 

Sommes, Moyennes et Produits

• Écrire un code avec une boucle for qui calcule la somme des entiers entre 1 et 12.
• Comparer le résultat précédent avec la fonctions np.sum.
• Écrire un code avec une boucle for qui calcule la moyenne des entiers entre 1 et 12.
• Comparer le résultat précédent avec la fonctions np.mean.
• Écrire un code avec une boucle for qui calcule le produit des entiers entre 1 et 12.
• Comparer le résultat précédent avec la fonction np.prod.

# Réponse 

Algèbre linéaire

Soit la matrice $A$ définie par : $$ A =\left( {\begin{array}{ccccc} 1 & 3 & 3 \\ -2 & 11 & -2 \\ 8 & -7 & 6 \\ \end{array} } \right) $$

• Calculer le déterminant de A et l'afficher.
• Calculer les valeurs propres $\lambda_i$ de A et les afficher.
• Calculer les vecteurs propres $v_i$ et les afficher sous forme d'une matrice où chaque colonne contient un $v_i$.
• A l'aide d'une boucle calculer pour chaque $i$ la norme $|| A v_i - \lambda_i v_i ||$. Écrire une phrase de conclusion.

Indications : Le déterminant, les valeurs propres, les vecteurs propres d'une matrice et la norme d'un vecteur se calculent respectivement avec les fonctions det,eigvals,eig,norm. Notez que eig renvoie deux valeurs : les valeurs propres et les vecteurs propres. Les vecteurs propres sont les colonnes de la matrice renvoyée.

# Réponse 

Courbes paramétrées

Reproduisez la figure avec une spirale algébrique (Archimédienne) et une spirale logarithmique, dans deux sous graphiques l'un à coté de l'autre. Comme sur la figure ci-dessous:

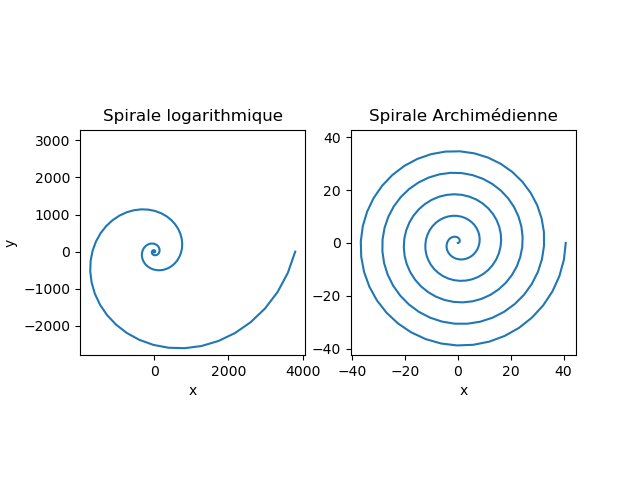
On peut définir des spirales avec $x = r \cos(\theta)$ et $y = r \sin(\theta)$, mais le rayon $r$ dépend de l'angle $\theta$. Pour la spirale logarithmique, on a la loi $r = a^\theta$ et pour la spirale Archimédienne on a $r = a \theta$, où $a$ est un paramètre fixe que l'on prendra égal à 1.3.

$\theta$ varie de 0 à $2 \pi$ pour un tour de spirale, et par exemple de 0 à $10 \pi$ pour 5 tours de spirale.

# Réponse