Les logiques¶
Combiné avec la "vectorisation", l'utilisation des logiques permet de réaliser des opérations complexes avec une syntaxe intuitive, très compacte et élégante. Il est ainsi possible de remplacer par une seule instruction une opération qui nécessiterait de combiner à la fois des tests et des boucles. La syntaxe est proche du langage mathématique mais il faut bien comprendre le fonctionnement interne des opérations avec les logiques pour éviter de mauvaises surprises.
Premier exemple¶
Pour introduire les possibilités des logiques, le plus simple est de prendre un exemple :
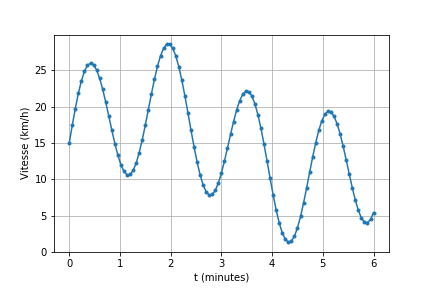Sur cette figure, je représente une vitesse en fonction du temps qui a été créée à l'aide des lignes de code ci-dessous. Imaginons que c’est la vitesse d’un cycliste en VTT mesurée pendant 6 minutes. La mesure est effectuée toutes les 5 secondes, il y a donc 73 mesures.
import numpy as np
import matplotlib.pyplot as plt
t = np.linspace(0,6,73)
v = 5*(np.sin(t) + 1.8*np.sin(4*t) + 3)
Je souhaite extraire la vitesse sur un temps compris entre 1 et 3 minutes et mettre cette partie en noir en trait épais sur la courbe. Pour cela, je fais tout d'abord un vecteur que j’appelle tcut.
tcut = t[(t>=1) & (t<=3)]
Je fais aussi un vecteur vitesse tronqué vcut qui correspond au même temps c-à-d tel que $t\ge 1$ et $t\le3$.
vcut = v[(t>= 1) & (t <= 3)]
Notez ici qu’entre les crochets [ ] devant v et devant t, j’ai mis, à la place d’indices ou des sections de tableau dont on a l'habitude, des expressions quasiment en langage naturel. "Je veux que la vitesse vcut soit égale à la vitesse v pour t compris entre 1 et 3".
Je peux superposer les courbes.
plt.plot(t,v,'.-')
plt.plot(tcut,vcut,'k',lw=3)
plt.grid()
plt.ylabel('Vitesse (km/h)')
plt.xlabel('t (minutes)')
plt.show()
On obtient bien le résultat voulu. Maintenant supposons que je veux mettre en vert les vitesses au-delà de 20 km/h et en rouge celles en dessous de 10 km/h. Pour être encore plus compact, je ne me sers plus de vecteur intermédiaire comme tcut et vcut mais je tape directement les expressions à l’intérieur du plot.
vrapide = 20
vlente = 10
plt.plot(t,v,'.-')
plt.plot(t[v>=vrapide],v[v>=vrapide],'go',lw=3)
plt.plot(t[v<vlente],v[v<vlente],'ro',lw=3)
plt.grid()
plt.ylabel('Vitesse (km/h)')
plt.xlabel('t (minutes)')
plt.show()
Je souhaite savoir pendant combien de secondes, le cycliste a réussi à être au delà des 20 km/h.
print("Le cycliste a été au delà de 20 km/h pendant : "+str(5*np.sum(v>20))+" secondes.")
# La somme est multipliée par 5 car les mesures sont prises toutes les 5 secondes.
On constate que cette écriture est très compacte et particulièrement efficace. Faire la même opération avec boucles et tests est possible mais aurait considérablement alourdi le code. Tout ceci n'est pas aussi magique que cela en a l'air. Il faut bien en comprendre les rouages pour bien l'utiliser.
Le principe de fonctionnement¶
Il faut comprendre les bases des logiques, on doit revenir à des notions très simples. En général, on crée un logique en écrivant une condition. Par exemple une inégalité ($3>4$) qui est ici fausse:
3>4
On peut étendre cela a un tableau numpy (vecteur, matrice ...)
x = np.array([5,1,4,6])
monTabLogic = x>=4
print(monTabLogic)
On a créé un vecteur de logiques monTabLogic avec la condition vraie ou fausse selon les positions dans le tableau. Grâce à ces positions, on peut extraire les valeurs x qui satisfont cette condition l'instruction
x[x>=4]
On récupère uniquement les valeurs de x aux indices où le tableau de logiques x>=4 est vrai. De même, en une seule instruction, je peux modifier toutes les valeurs de x supérieures ou égales à 4 en leur assignant la valeur 9.
x[x>=4] = 9
print(x)
Le vecteur x est maintenant modifié.
Pour pouvoir compter le nombre d'occurences où la condition est vraie, on peut se servir de np.sum car de manière interne la condition logique stockée sur un bit vaut 1 quand la condition est vraie et 0 quand elle est fausse. Par exemple :
print("Il y a "+str(np.sum([True, False, True, True]))+" éléments 'True' dans ce tableau.")
Combiner des conditions logiques:¶
Il est fréquent de combiner plusieurs conditions logiques. Les tests peuvent être coûteux en terme de temps de calculs et c'est pourquoi sous Python la notion de test "racourci" a été créée.
Dans le premier exemple, on a combiné deux conditions : $t \ge 1$ et $t \le 3$. Le mot clé utilisé n'est pas and comme on pourait s'y attendre mais un &. Le and est un test dit "short-circuit" et le & est un test dit "bitwise". Le "short_circuit" cesse la séquence de tests dès que la condition logique de l'ensemble est vérifiée. Par exemple, on souhaite connaître le résultat de : $3>4$ and $7<8$. On teste tout d'abord $3>4$ qui est faux, il est inutile de perdre du temps à tester $7<8$ car quelque soit le résultat de ce deuxième test, l'ensemble sera faux. Dans notre exemple sur la vitesse avec des tableaux numpy, on veut tester toutes les positions pour récupérer les indices. On force ainsi Python à faire tous les tests grace au test bitwise. La syntaxe est différente suivant le type de test :
- Short-circuit : and, or, not.
- Bitwise : &,|,~.
Une régle un peu pragmatique et facile à retenir est qu'on utilise en général les tests short-circuit avec les instructions if ou les boucles while et les tests bitwise pour les tableaux numpy.