Lecture et exploitation d'images

Ces notes sur la lecture et exploitation d'images reprennent très largement des idées de Jérôme Hoepffner pour un cours utilisant Matlab. Elles ont été adaptées à Python.

A partir d'une expérience physique capturée par une photographie, nous allons mesurer des quantités pour les analyser ensuite. Nous allons lire une image sur le disque dur puis l'afficher dans une fenêtre graphique. Cette image est en fait un tableau avec un grand nombre de pixels : chaque point de l’image est repéré par les coordonnées du pixel correspondant. C’est ainsi qu’un appareil photo peut être un instrument de mesure extrêmement précis : d’autant plus précis que son capteur dispose d’un grand nombre de pixels. Nous allons étudier la forme d’un coquillage. On montrera par la suite que ce coquillage ressemble beaucoup à une spirale logarithmique. L’image est stockée dans le fichier ”nautile.png”. Le plus simple est de placer ce fichier dans le répertoire courant sur lequelle spyder pointe. On peut vérifier la présence du fichier image ("nautile.png" par exemple) avec la commande unix ls que l'on tape dans la console ipython de spyder. La fonction imread de la bibliothèque imageio permet de relire et transférer l'image dans un tableau numpy. La fonction imshow de matplotlib de l'afficher.

Bibliothèques et réglage préliminaire de spyder

• Bibliothèques : imageio, numpy et matplotlib.pyplot

• Si vous ne l'avez pas encore fait, il devient indispensable d'afficher les figures dans des fenêtres indépendantes (fenêtres graphiques interactives), dans spyder, il convient de faire le réglage suivant : Outils-> Préférences -> Console IPython -> Graphiques et régler "Sortie graphique" sur "automatique"

Réglage en vidéo

Ensuite, on redémarre Spyder pour que ces modifications soient prises en compte.

Note : Ceux qui utilisent jupyter notebook (ce qui n'est pas recommandé pour ce cours) il faut rajouter la ligne magique : %matplolib auto

Prise de mesures sur une image

import numpy as np
import imageio.v2 as imageio  # import imageio # fonctionne aussi
import matplotlib.pyplot as plt

# on lit l’image dans le tableau monimage 
monimage=imageio.imread('nautile.png')

# On affiche cette image avec matplotlib
plt.imshow(monimage)
plt.axis('equal')
plt.xlabel('colonnes')
plt.ylabel('lignes')
plt.title('mon image')
plt.show()

On note que les axes sont numérotés en pixels : il y a un peu plus de 450 pixels dans la direction horizontale et un peu moins de 450 pixels dans la direction verticale. Nous verrons dans un instant qu'il y a exactement 429x462 pixels dans cette image. L’origine de la numérotation est en haut à gauche de l’image, et on note de plus que l’axe vertical est orienté de haut en bas. En termes de référentiel, cela signifie que le référentiel de l’image a son centre en haut à gauche de l’image, que l’échelle de longueur est le pixel et que l’axe des y est à l’envers par rapport au graphique cartésien habituel en mathématiques. Ce référentiel est représenté ci-dessous en couleur cyan et les axes sont nommés ”xpixel” et ”ypixel”.

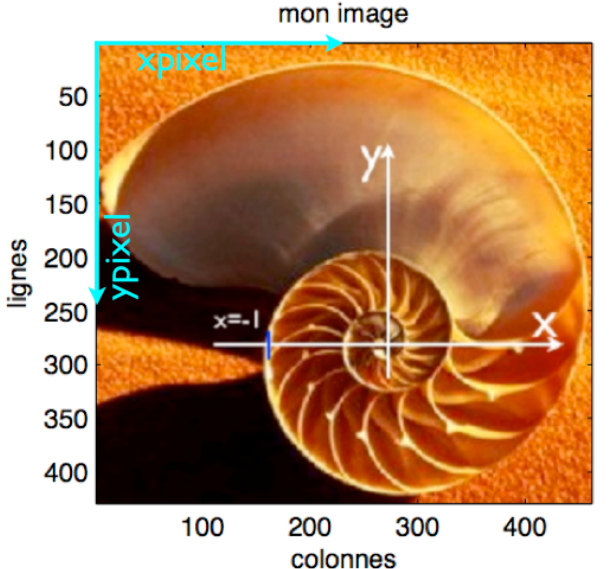
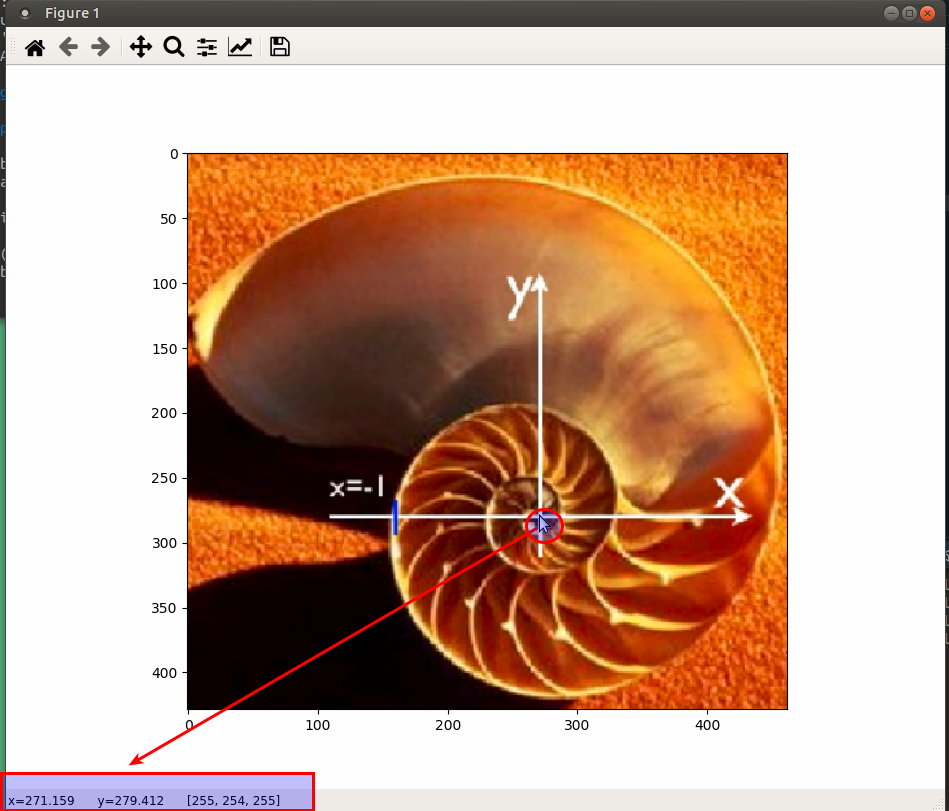
Nous allons maintenant mesurer la forme de ce coquillage en prenant une vingtaine de points de mesure le long de la ligne spirale. Pour cela, nous pouvons par exemple relever les pixels grâce à la fenêtre interactive que matplotlib a ouvert pour nous. En promenant le curseur de la souris, les coordonnées du pixel et le code RGB de la couleur de ce pixel s'affichent en bas à gauche de la fenêtre (suivant la version de matplotlib cela peut être en haut à droite). Sur la capture d'écran ci-dessous, la pointe de la petite flèche blanche (mise en évidence par le cercle rouge) montre que la souris est positionnée très proche du centre du coquillage. Elle montre l'origine des axes blancs qui ont été rajoutés sur la photo. Comme on peut le voir dans le rectangle rouge, le pixel a pour coordonnées x=271.159 et y=279.412 dans les axes cyan. En arrondissant à l'entier le plus proche, la souris est sur le pixel (271,279). Ce pixel a pour code RGB (255,254 255). Le code RGB décrit la couleur en spécifiant la proportion de rouge (R pour ”red”) de vert (G pour ”green”) et bleu (B pour ”blue”). Les valeurs entières vont de 0 à 255 (image codée sur 8 bits $2^8=256$ niveaux). Ce pixel est donc quasiment blanc car Rouge et Bleu sont au maximum et le vert est à 254.

Si vous tapez la commande print(monimage.shape), vous allez obtenir le tuple (429,462,3). monimage est donc un tableau à trois dimensions les deux premières dimensions correspondent au nombre de pixels de l'image et la troisième dimension aux trois couleurs R, G et B. Cette image en couleur est un "empilement" de trois tableaux (429,462) contenant les niveaux entre 0 et 255 pour R, G et B.

Pour mesurer la position d’une vingtaine de points sur la coquille, on pourrait positionner la souris successivement sur 20 points et noter les coordonnées, mais nous avons pour cela un outil plus pratique, la fonction plt.ginput. La fonction plt.ginput est une fonction interactive dont le nom est un raccourci pour ”graphical input”, (entrée graphique). En général, on ne la met pas dans un script, mais on la tape dans la console IPython. En effet, lors du développement de notre projet, on est amené à exécuter de nombreuses fois le script en cours d'élaboration : pour l’améliorer, pour éliminer les erreurs, pour tester de nouvelles idées. Par contre, il suffit de faire la prise de mesure une bonne fois pour toute, et de sauver les données quelque part. A chaque fois que l’on appelle la fonction ”ginput”, il faudrait cliquer pour la prise de mesures. Nous allons voir deux techniques pour éviter de refaire les prises de mesure.

Si on souhaite faire les mesures sur le coquillage :

coord=plt.ginput(20,60.0) Il y a deux arguments à ginput :

• le nombre de points maximum que je veux saisir. C'est un entier ici 20.
• le temps maximum que je me donne pour le faire. C'est un float ici 60.0 secondes.

On ajoute un point avec un clic gauche. On supprime le dernier point saisi avec un clic droit (ou 'del' au clavier). Si le temps s'est écoulé, on ne récupère que le nombre points saisis jusque là. La sortie de la fonction est ici envoyée dans coord

coord une liste de tuples ce qui n'est pas très pratique pour faire des calculs par la suite. On préfère récupérer directement un array numpy. C'est très simple à faire, il suffit d'écrire la commande coord=np.array(plt.ginput(20,60.0)) qui convertit la sortie de ginput en array numpy.

Une fois que j’ai mesuré les coordonnées de ces points dans le tableau coord, je peux les sauver sur le disque dur dans le fichier 'coordonnees.dat' avec la fonction de numpy np.savetxt('coordonnees.dat',coord). Pour relire ce tableau depuis le fichier 'coordonnees.dat', on se sert de la commande coord = np.loadtxt('coordonnees.dat'). Nous aurions pu changer le nom du tableau dans lequel on fait la relecture par exemple coord_bis = np.loadtxt('coordonnees.dat').

Pour relire un fichier, comme pour les images à lire, il faut toujours s'assurer qu'il est bien dans le répertoire courant.

# Decommenter les deux lignes suivantes pour faire la saisie la première fois 
#coord = np.array(plt.ginput(20,60.0))
#np.savetxt('coordonnees.dat',coord)
# Relecture dans le fichier coordonnees.dat
coord = np.loadtxt('coordonnees.dat')

Nous vous conseillons donc le cycle suivant. La première fois que vous executez votre script, vous enchainez les commandes plt.ginput et np.savetxt. Si vous êtes satisfait de votre saisie de points, vous commentez ces deux lignes et ne laissez que la ligne contenant load comme c'est le cas ci-dessus.

Note : Il est possible d'automatiser cette procédure avec un test sur l'existence du fichier dans le répertoire. Nous montrons ceci dans l'exemple suivant

Pour bien vérifier que nous avons bien pris les points de mesure, nous pouvons tracer par dessus l’image les points de coordonnées ”xpixel” et ”ypixel” en les extrayant du tableau numpy coord.

xpixel = coord[:,0] # On extrait dans xpixel la première colonne de coord
ypixel = coord[:,1] # On extrait dans ypixel la deuxième colonne de coord
plt.imshow(monimage)
plt.plot(xpixel,ypixel,'o-b',lw=2)
plt.show()

Changement de référentiel

Les coordonnées que nous avons mesurées sont exprimées dans le référentiel des pixels de l’image, qui n’est pas pratique pour la comparaison avec des expressions mathématiques. Nous devons donc effectuer un changement de référentiel. Sur l’image du Nautile, nous avons représenté en blanc les axes d’un référentiel physique et une référence de longueur (la position du -1 sur l’axe des abscisses). C’est dans ce référentiel là que nous voulons manipuler nos données. Voici les opérations de ce changement de référentiel :

# Centre du référentiel
xpixel0 = 271
ypixel0 = 279
x = xpixel - xpixel0
y = ypixel - ypixel0

# On inverse l'axe vertical
y = -y

# On définit la taille d'un pixel grace à l'échelle
taillepix = 1/(271-161)  # 1 cm pour (271 - 161) pixels

# On fait la mise à l'échelle
x = x*taillepix
y = y*taillepix

La première chose que nous avons faite est de mesurer sur la figure les coordonnées du centre du référentiel physique avec la souris en zoomant éventuellement. Les coordonnées du centre du référentiel physique sont stockées dans les variables ”xpixel0” et ”ypixel0”. Ensuite nous avons soustrait ces coordonnées aux coordonnées des points mesurés. Cette soustraction c’est la translation de la courbe vers le centre du référentiel physique. Ensuite nous avons inversé l’axe des ”y”. En effet l’axe vertical des pixels est gradué de haut en bas et non pas de bas en haut. Ensuite nous avons mesuré la taille d’un pixel en unités de longueur physique. Pour cela nous disposons d’un étalon de longueur : la position ”-1” indiquée sur l’image. Elle nous indique 1 centimètre. Je mesure la taille en pixel de la distance entre ce point ”x=-1 cm” et le centre du référentiel, et cela me donne la taille physique d’un pixel. Cette taille est stockée ici dans la variable ”taillepix”. La dernière opération à réaliser pour le changement de référentiel est maintenant de multiplier les coordonnées de mes points mesurés par ”taillepix”. Je peux maintenant tracer mes points de mesures dans le référentiel physique.

# On trace la spirale
plt.plot(x,y,'b-*')
plt.xlabel('x (cm)')
plt.ylabel('y (cm)')
plt.grid()
plt.axis('equal')
plt.title('points mesurés dans le référentiel physique')
plt.show()

Cette figure montre bien que nous avons effectué correctement le changement de référentiel : le point (0, 0) est bien au centre de la spirale, preuve que nous avons bien translaté les coordonnées, la courbe n’est pas "retournée", preuve que nous avons bien inversé l’axe vertical, et l’échelle est bonne puisque la seconde spire de la spirale est de taille à peu près 1 cm. Maintenant je peux tracer par dessus mes points de mesure une spirale logarithmique pour comparer les formes. Pour ma spirale théorique, j’ai besoin d’identifier les deux paramètres ”a” et ”b” de la formule :

$$ r = ab^\theta, x = r \cos(\theta), y = r \sin(\theta) $$

où $\theta$ et $r$ sont les coordonnées polaires de ma courbe. Nous verrons plus loin comment estimer la valeur d’un paramètre d’une formule mathématique à partir de mesures sur une image. A ce stade, nous prenons des valeurs déterminées à l'avance pour a et b.

plt.plot(x,y,'b-*')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Comparaison entre mesures et théorie')
# on trace une spirale théorique
th = np.linspace(0,2*np.pi*2.5,500)
a = 0.1471
b = 1.213
r = a*(b**th)
xtheo = r*np.cos(th)
ytheo = r*np.sin(th)
plt.plot(xtheo,ytheo,'k-',lw=2)
plt.axis('equal')
plt.grid()
plt.show()

On observe un bon accord entre la formule théorique et la forme du coquillage. C’est une indication que le coquillage croı̂t de façon récursive : le mollusque qui l’habite agrandit sa coquille lorsqu’il a grandi lui-même, et il agrandit sa coquille en proportion de sa propre taille.

Mesures sur une image multiple

Dans l’exemple que nous venons de traiter il y a juste une image statique et nous mesurons une forme sur cette image. En général en physique, nous nous intéressons à comment une grandeur physique dépend d’un paramètre. Par exemple pour une balle en chute libre, on s’intéresse à la hauteur de la balle en fonction du temps (le paramètre qui varie c’est le temps). Dans ce cas là on capture le phénomène grâce à un film. On peut transformer ce film en une image multiple en mettant les unes à côté des autres les images du film. La figure ci-dessous représente quatre exemples d’images multiples :

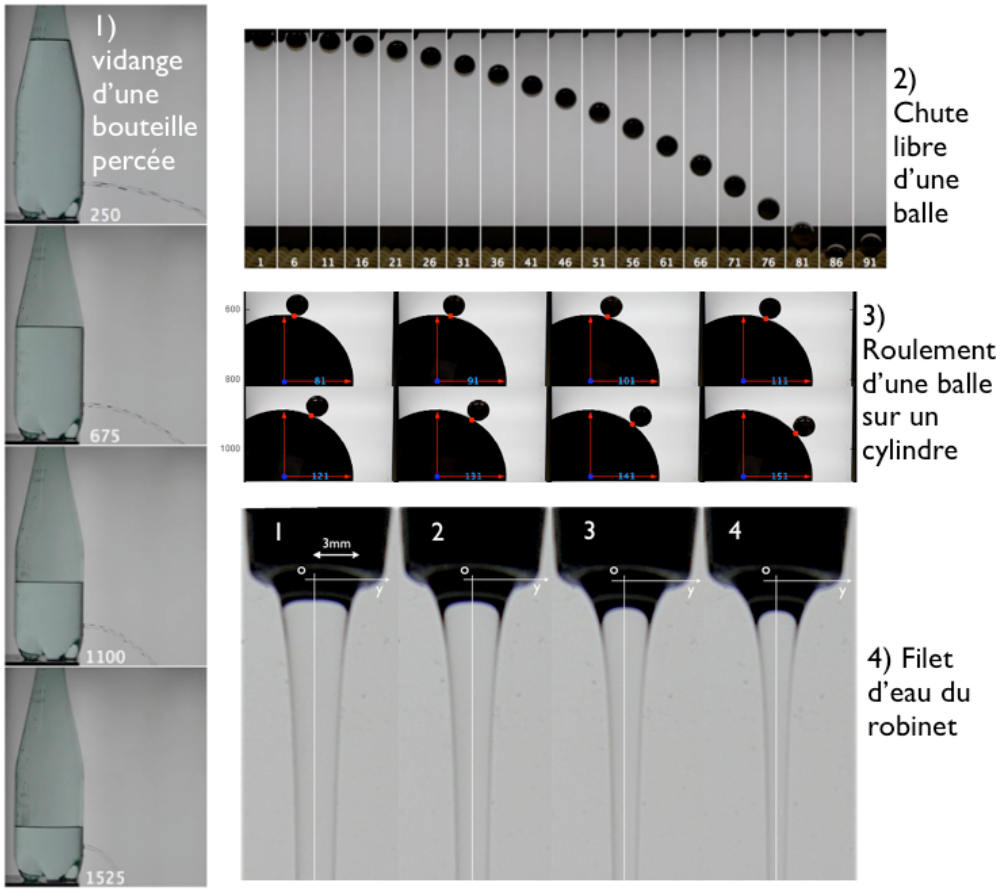
Les trois premiers exemples représentent les temps successifs du film du phénomène : comment le niveau d’eau varie lorsqu’une bouteille se vidange par un trou (problème de Torricelli, mécanique des fluides, niveau L2, la chute libre d’un corps (mécanique du point, niveau L1), le roulement d’une balle sur un cylindre (dynamique du solide rigide, niveau L3). La quatrième image concerne la forme du filet d’eau qui coule d’un robinet (mécanique des fluides, niveau L2). Les images successives représentent non pas comment ce filet d’eau change dans le temps, mais comment il change lorsqu’on diminue le débit progressivement en fermant petit à petit le robinet. Nous allons traiter ici le cas de la chute libre d’une balle. La première chose à faire est de prendre les points de mesure sur l’image, comme décrit plus haut.

#Lecture du fichier chute libre:
imcl=imageio.imread('chutelibre.png')

# Prise de mesure : version plus sophistiquée avec un test sur l'existence du fichier
import os
filename = 'coordonneeschutelibre.dat'
if os.path.exists(filename):
    # Ne mettre la ligne magique ci dessous que sur jupyter notebook 
    %matplotlib inline 
    print('Je relis les coordonnées dans le fichier '+filename)
    coord = np.loadtxt(filename)
else :
    print('Saisir les coordonnées sur la figure')
    # Ne mettre la ligne magique ci dessous que sur jupyter notebook
    %matplotlib auto  
    plt.imshow(imcl)
    coord = np.array(plt.ginput(17,50.0))
    np.savetxt(filename,coord)

Je relis les coordonnées dans le fichier coordonneeschutelibre.dat

xpixel = coord[:,0] # On extrait dans xpixel la première colonne de coord
ypixel = coord[:,1] # On extrait dans ypixel la deuxième colonne de coord
plt.imshow(imcl)
plt.plot(xpixel,ypixel,'+-r',lw=1)
plt.show()

Sur l’image, plutôt que de mesurer la position du centre de la balle, j’ai mesuré la position du bas de la balle parce que c’est plus précis (c’est difficile de voir sur l’image où se situe le centre). Je vais maintenant effectuer le changement de référentiel. Pour les ”y” la procédure est la même que décrit plus haut : je prends comme origine du référentiel la première position de la balle, comme cela ma courbe va commencer à y = 0. Par contre, il y a une différence pour le traitement de l’axe des x : la coordonnée x des points de mesure ne me sert ici à rien, puisque chacun de mes points de mesure correspond à un temps différent : dans mon graphique final je trace la hauteur de chute en fonction du temps. Il faut donc construire le vecteur des temps successifs du film. Le numéro affiché sur chacune des images correspond au numéro de l’image dans le film : 1,6,11,16..., 81 c’est à dire que nous avons pris les images de 1 à 81 en ne conservant qu'une image sur 5. On ne se sert pas des images 86 et 91. Ce film est enregistré à 300 images par seconde, le pas de temps est donc dt=1/300 c’est l’intervalle de temps entre deux images du film. Le vecteur des coordonnées temporelles est donc :

dt = 1/300
tvec = np.arange(0,81,5)
tvec = tvec*dt

Dans Python, le numérotation démarre à 0 ce qui est pratique ici. La premère image est donc associée au temps 0, l'image 6 au temps (6-1)/300=5/300 etc. Pour l'étalon de longueur, nous savons que la hauteur de la fenêtre lumineuse est de 35 cm, nous pouvons en déduire la taille d’un pixel. Après conversion on obtient un graphique de la hauteur en fonction du temps.

taillepix = 0.35/(373-10)
h = (ypixel-ypixel[0])*taillepix

plt.plot(tvec,h,'o-')
plt.xlabel('temps (s)')
plt.ylabel('hauteur (m)')
plt.grid()

Comparer une courbe expérimentale à une formule mathématique

Les expériences nous donnent des points de mesure que nous pouvons tracer sur un graphique. Les modèles théoriques nous donnent des formules mathématiques qui dépendent de paramètres physiques. Pour la chute libre d’un corps, le seul paramètre physique est l’accélération de la gravité g. La formule théorique est :

$$ h = \frac{1}{2} g \ t^2 $$

Nous ajoutons la comparaison

g = 9.81

plt.plot(tvec,h,'x')
plt.plot(tvec,0.5*g*tvec**2,'r--')
plt.xlabel('temps (s)')
plt.ylabel('hauteur (m)')
plt.grid()
plt.title('Chute libre : Comparaison avec la théorie')
plt.show()

On voit que la correspondance est très bonne entre l’expérience et la théorie. Souvent, on ne connaı̂t pas la valeur numérique des paramètres physiques dans une formule mathématique. La comparaison entre la formule théorique et les mesures expérimentales sont alors un moyen pour déterminer la valeur de ce paramètre physique. Supposons par exemple que nous ne connaissons pas la valeur de g et que nous utilisons notre expérience pour la mesurer. Je peux tester la formule pour plusieurs valeurs de g en faisant une boucle :

gvec = np.linspace(1,15,10) # On teste 10 valeurs de g entre 1 et 15

for g in gvec:
    plt.plot(tvec,0.5*g*tvec**2,'r--')
plt.xlabel('temps (s)')
plt.ylabel('hauteur (m)')
plt.plot(tvec,h,'*b',label='courbe exp.')
plt.grid()
plt.legend()
plt.title('Comparaison avec la théorie pour g variable')
plt.show()

On remarque que la courbe pour la septième valeur de g (qui vaut 10.333) s'approche assez bien de la courbe expérimentale. Il est aussi possible de quantifier précisément l’écart entre les données expérimentales et une formule théorique pour une valeur des paramètres physiques. Voici une figure qui montre cet écart :

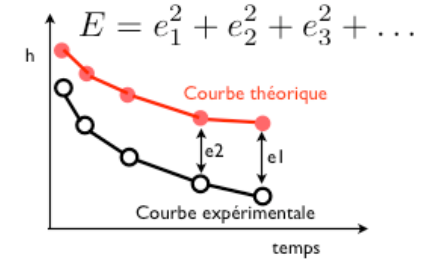
Pour chaque point de mesure numéro i, on calcule le carré $e_i^2$ de la distance entre le point expérimental et la formule théorique. On fait la somme de tous ces écarts dans E qui devient ainsi une mesure globale de l’écart. $$ E = \sum_{i=1}^N (h_{theo}(t_i) - h_{expe}(t_i))^2 \mbox{ où N est le nombre de points expérimentaux} $$ Si E est nul, alors la courbe théorique est exactement sur la courbe expérimentale. Par contre, plus E sera grand, plus la distance entre la formule théorique et la courbe expérimentale sera grande (c’est à dire que la valeur de g associée sera d’autant plus fausse). Pour ce calcul, nous pouvons nous servir de ce que nous avons vu lors de la vectorisation (même si il est toujours possible d'utiliser des boucles). Voici les instructions qui calculent cet écart E entre la mesure de la chute libre et la formule théorique pour plusieurs valeurs de g que nous supposons inconnue.

# On "prépare" nos vecteurs en ligne ou en colonne
gvec = gvec[:,np.newaxis] # transforme gvec en vecteur colonne
tvec = tvec[np.newaxis,:] # transforme tvec en vecteur ligne
h = h[np.newaxis,:] # transforme h en vecteur ligne

Htheo = 0.5*gvec*tvec**2  # On fait ici du broadcasting

E = np.sum( (Htheo - h)**2,axis=1 ) # Notez bien dans cette ligne
                                    # 1) Le broadcasting pour Htheo - h 
                                    # 2) Le choix de axis pour la somme.
plt.plot(gvec,E,'*') 
plt.xlabel('g (m/s^2)')
plt.ylabel('Ecart E')
plt.grid()
plt.show()

On voit bien, que l’écart devient très petit pour $g$ proche de 10. Pour des valeurs inférieures ainsi que pour des valeurs supérieures, l’écart devient très grand. Pour mesurer avec plus de précision la valeur de g qui est la plus compatible avec nos données expérimentales, il est possible de raffiner notre courbe avec 50 valeurs de g entre 9.5 et 10.2 et tracer l’erreur en échelle semi-logarithmique :

gvec = np.linspace(9.5,10.2,50)
gvec = gvec[:,np.newaxis]

Htheo = 0.5*gvec*tvec**2 

E = np.sum( (Htheo - h)**2,axis=1 ) 

plt.semilogy(gvec,E,'*') 
plt.xlabel('g (m/s^2)')
plt.ylabel('Ecart E')
plt.grid()
plt.show()

print("Le minimum est trouvé pour l'indice ", np.argmin(E))
print("La valeur qui minimise l'écart est trouvée pour g = ", str(gvec[np.argmin(E),0]) ," m/s^2" )

Le minimum est trouvé pour l'indice  22
La valeur qui minimise l'écart est trouvée pour g =  9.814285714285713  m/s^2

Ici, on voit que l’erreur n’atteint jamais zéro, effectivement il y a une petite erreur de mesure (position exacte de la balle, identification du temps initial...) et des effets physiques qui ne sont pas pris en compte dans la modélisation (friction de l’air, ...). Le minimum de l’erreur est pour g très proche de la valeur de 9.81.