Le broadcasting¶
L'utilisation du broadcasting permet de s'affranchir de nombreuses boucles for. Une bonne maitrise du broadcasting permet de gagner en terme de compacité et surtout d'efficacité dans les codes que vous allez écrire. Il faut cependant être assez prudent avec cet outil puissant. Une bonne compréhension des axes (avec np.newaxis) ou de la fonction np.reshape() est indispensable. Il faut être vigilant avec les dimensions de vos tableaux.
Sans le savoir, on fait assez naturellement du broadcasting. Par exemple si A est une matrice, on peut calculer A + 2.0 alors que 2.0 n'a pas la même dimension que A.
import numpy as np
A = np.array([[8,1,6],[3,5,7],[4,9,2]])
A + 2.0
Ce qui serait cohérent d'écrire ce serait :
A + 2.*np.ones(np.shape(A)) # On sommerait ainsi deux matrices de même "shape" (ou conformante).
C'est lourd en écriture et numpy se charge de faire cela pour vous. Le A + 2.0 est "intuitif" et plutôt simple à comprendre.
Regardons maintenant les opérations suivantes:
v1 = np.array([1,3,5,7]) # Je crée un vecteur v1 avec 4 éléments
v2 = np.array([2,4,6]) # Je crée un vecteur v2 avec 3 éléments
Notez qu'à ce stade, v1 et v2 ne sont ni des vecteurs lignes, ni des vecteurs colonnes. Leur shape est (4,) et (3,) respectivement et par exemple np.dim(v1) vaut 1. Cela veut dire qu'ils ont 4 et 3 éléments sans précision sur le nombre de lignes ou de colonnes.
Si on fait l'opération
v1 + v2
on obtient une erreur:
Ce que l'on peut comprendre car v1 et v2 n'ont pas le même nombre d'éléments.
Maintenant avant de faire l'addition, on va redimensionner v1 en vecteur colonne et v2 en vecteur ligne avec la commande reshape. Il serait plus rigoureux de dire que l'on va créer une matrice avec une seule colonne (ou une seule ligne).
v1 = np.reshape(v1,(4,1))
v2 = np.reshape(v2,(1,3))
Dans un code, on écrirait plutôt de manière générique : v2 = np.reshape(v2,(1,np.size(v2))) (ici np.size(v2) = 3.)
Regardons maintenant le résultat de la somme de v1 + v2:
print(f"Somme de v1 et v2 : \n {v1+v2}")
C'est assez étonnant car v1 et v2 n'ont pas la même taille. En faisant la somme de
$$ \begin{pmatrix} 1 \\ 3 \\ 5 \\ 7 \end{pmatrix} + \begin{pmatrix} 2 & 4 & 6 \end{pmatrix} $$
on a obtenu une matrice (4,3) $$ \begin{pmatrix} 3 & 5 & 7 \\ 5 & 7 & 9 \\ 7 & 9 & 11 \\ 9 & 11 & 13 \end{pmatrix} $$
qui est la somme de deux matrices suivantes:
$$ \begin{pmatrix} 1 & 1 & 1 \\ 3 & 3 & 3 \\ 5 & 5 & 5 \\ 7 & 7 & 7 \end{pmatrix} + \begin{pmatrix} 2 & 4 & 6 \\ 2 & 4 & 6 \\ 2 & 4 & 6 \\ 2 & 4 & 6 \end{pmatrix} $$
Pour mieux comprendre ce qui s'est passé, il faut regarder :
- Soit ces deux vidéos en anglais :
- Soit, dans un style très différent, les 10 premières minutes de la vidéo en français :
Après avoir visionné ces vidéos, vous devez avoir
compris l'importance de la fonction np.reshape pour faire du broadcasting.
np.newaxis :
Il est donc indispensable de redimensionner les tableaux avant de faire du broadcasting. Ne pas le faire peut engendrer des erreurs quand on l'excécute ou, bien pire encore, vous pouvez écrire un script qui ne provoque pas d'erreur mais fait des opérations différentes de ce que vous souhaitiez !
La syntaxe avec le np.reshape est cependant un peu lourde. Nous l'avons introduite car son utilisation reste répandue. Dans les versions plus récentes de numpy, l'utilsation de np.newaxis permet d'alléger l'écriture et la lisibilité du code. Nous l'utiliserons dans ce cours.
Reprenons les deux vecteurs v1 et v2.
v1 = np.array([1,3,5,7])
v2 = np.array([2,4,6])
print(f"Shape de v1 : {v1.shape} ")
print(f"Shape de v2 : {v2.shape} ")
Au lieu d'écrire : v1 = np.reshape(v1,(np.size(v1),1)) et v2 = np.reshape(v2,(1,np.size(v2))). On peut écrire directement une commande avec np.newaxis qui produit le même résultat.
v1 = v1[:,np.newaxis] # Observez bien où se trouve le np.newaxis par rapport au :
v2 = v2[np.newaxis,:] # pour v1 il est à droite et pour v2 il est à gauche.
print(f"Shape de v1 : {v1.shape}")
print("Shape de v2 : ", v2.shape)
print(f"Somme de v1 et v2 : \n", v1+v2)
Applications pratiques :¶
Nous allons utiliser les capacités de broadcasting de python pour calculer des séries ou faire des graphiques sans utiliser de boucles.
On introduit tout d'abord une fonction supplémentaire : np.cumsum qui permet de faire une somme cumulée.
Par exemple :
v = np.arange(1,5)
print("v = \n",v)
np.cumsum(v)
cumsum a créé le vecteur 1, 1+2,1+2+3,1+2+3+4 en cumulant les éléments de v.
np.cumsum peut aussi s'appliquer sur des matrices avec le même principe de fonctionnement que np.sum en ce qui concerne les axes.
print("A= \n",A)
print("Cumsum suivant l'axe 0 = \n",np.cumsum(A,0))
print("Cumsum suivant l'axe 1 = \n",np.cumsum(A,1))
Calcul du développement limité de la fonction exponentielle autour de 0¶
Prenons le calcul exact de $e^x$ pour 5 valeurs de $x$ comprises entre 0 et 1
x = np.linspace(0,1,5)
np.exp(x) # C'est le calcul exact avec la fonction np.exp
Vérifions si $$ expN = 1 + x + \frac{x^2}{2!} + \cdots = \sum_{n=0}^N \frac{x^n}{n!} + \cdots $$ approche correctement exp(x) en ne retenant que les trois premiers termes de la série:
n = np.arange(3)
n = n[:,np.newaxis] # n est maintenant un vecteur colonne de shape (3,1)
x = x[np.newaxis,:] # x est maintenant un vecteur ligne de shape (1,5)
Grace à np.newaxis on dispose des matrices x et n avec lesquelles on peut faire du broadcasting.
Note : La fonction factorial existe dans la bibliothèqe math mais elle ne sait pas gérer les tableaux numpy. On importe factorial d'une autre bibliothèque appelée scipy (scientific python).
from scipy.special import factorial # On importe uniquement factorial de cette bibliothèque et
# on peut alors utiliser factorial sans préfixe.
ExpN = x**n/factorial(n) # ici x**n est une matrice (3,5) et la division par factorial(n) ne modifie pas le shape.
print(ExpN)
Sur la première ligne de la matrice, on a la fonction 1, la deuxième $x$, la troisième $\frac{x^2}{2!}$.
Pour comprendre comme le broadcasting a fonctionné, on peut décomposer les étapes du calcul de ExpN.
Grace à np.newaxis on a un vecteur ligne x et un vecteur colonne n :
$$ x**n = \begin{pmatrix} 0 & 0.25 & 0.5 & 0.75 & 1 \end{pmatrix} ** \begin{pmatrix} 0 \\ 1 \\ 2 \end{pmatrix} $$
Avant de faire l'opération puissance $**$, le broadcasting crée virtuellement deux matrices (3,5) en "broadcastant" le vecteur ligne x et le vecteur colonne n comme ceci:
$$ \begin{pmatrix} 0 & 0.25 & 0.5 & 0.75 & 1 \\ 0 & 0.25 & 0.5 & 0.75 & 1 \\ 0 & 0.25 & 0.5 & 0.75 & 1 \end{pmatrix} ** \begin{pmatrix} 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 1 & 1 & 1 \\ 2 & 2 & 2 & 2 & 2 \end{pmatrix} $$
L'opération puissancese fait élément par élément. On obtient la matrice (3,5)
$$ \begin{pmatrix} 1. & 1. & 1. & 1. & 1. \\ 0. & 0.25 & 0.5 & 0.75 & 1. \\ 0. & 0.0625 & 0.25 & 0.5625 & 1. \end{pmatrix} $$
l'opération factorial est vectorisée ce qui fait que factorial(n) est un vecteur colonne de même dimension que n.
$$ \begin{pmatrix} 1 \\ 1 \\ 2 \end{pmatrix} $$
en divisant la matrice (3,5) $x**n$ par le vecteur colonne factorial(n), le vecteur colonne est broadcasté avant de faire une division élément par élément.
$$ \begin{pmatrix} 1. & 1. & 1. & 1. & 1. \\ 0. & 0.25 & 0.5 & 0.75 & 1. \\ 0. & 0.0625 & 0.25 & 0.5625 & 1. \end{pmatrix} / \begin{pmatrix} 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 \\ 2 & 2 & 2 & 2 & 2 \end{pmatrix} $$
On obtient alors le résultat demandé.
$$ \begin{pmatrix} 1. & 1. & 1. & 1. & 1. \\ 0. & 0.25 & 0.5 & 0.75 & 1. \\ 0. & 0.03125 & 0.125 & 0.28125 & 0.5 \end{pmatrix} $$
En utilisant sur cette matrice la fonction np.sum et en choissant l'axe 0, on obtient le résultat cherché que l'on peut le comparer au résultat exact.
print(f'Dev Limité de Exp pour x = {x}')
print(np.sum(ExpN,0))
print("à comparer au calcul exact")
print(np.exp(x))
Sans surprise, le DL est moins précis quand on s'écarte de 0.
Mais on peut aller plus loin avec np.cumsum. En prenant np.cumsum(ExpN,0) on obtient une matrice qui sur chaque ligne contient le première terme, la somme des deux premiers termes du developpement limité et on retrouve la somme des trois premiers termes sur la troisième ligne.
print(np.cumsum(ExpN,0))
On peut maintenant tracer toutes ces fonctions approchant exp(x) sans boucle.
import matplotlib.pyplot as plt
plt.plot(x.T,(np.cumsum(ExpN,0)).T)
plt.plot(x.T,np.exp(x).T,'--k') # solution exacte en noir pointillé.
plt.xlabel('x')
plt.show()
Remarque : Vous allez comprendre dans un instant pourquoi on a dû transposer avec .T au moment de faire les tracés.
Tracé de plusieurs courbes sans boucle avec plt.plot¶
Essayons d’obtenir la figure suivante sur laquelle il y a un sinus sur $[0, 4 \pi]$ qui est déphasé au fur et à mesure que l’ordonnée croit.
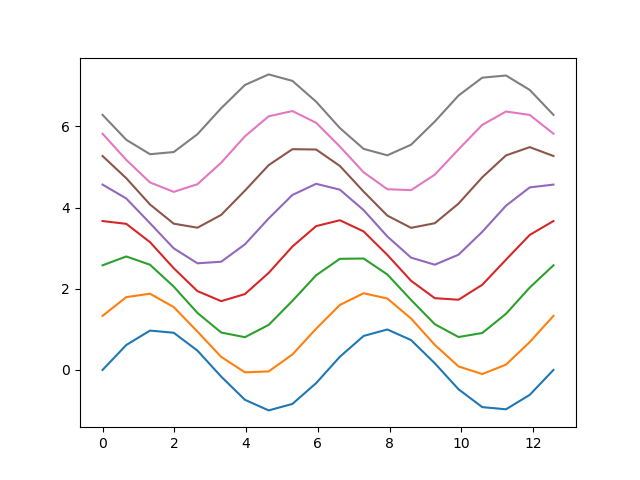
Avec linspace créons un vecteur colonne de 20 points x sur $[0, 4 \pi]$ et un vecteur ligne phase sur $[0, \pi]$ de 8 points.
x = np.linspace(0,4*np.pi,20)
x = x[:,np.newaxis]
phase = np.linspace(0,np.pi,8)
phase = phase[np.newaxis,:]
Grâce au broadcasting, nous pouvons maintenant créer la matrice Y avec le sinus déphasé et le déplacement de l’ordonnée ici que nous prenons un peu arbitrairement égale à deux fois la phase.
Y = 2*phase + np.sin(x+phase) # Ici l'operation x+phase qui crée la matrice
plt.plot(x,Y)
plt.savefig('sinusdephase.png')
plt.show()
La commande plot(x,Y) avec Y comme matrice en argument a tracé chaque colonne de Y en fonction de x. Python a privilégié le parcours du premier indice. C’est pour cela que pour le développement limité d’exponentiel, nous avons été obligé de transposer car petit x était un vecteur ligne. Ici, nous avons anticipé le tracé des courbes et nous avons pris soin de prendre dès le départ x comme un vecteur colonne.
Utilisation de np.tile() pour comprendre¶
L'utilisation du broadcasting se fait de manière implicite dans les exemples précédents. Pour mieux comprendre la logique des opérations effectuées, nous pouvons introduire la fonction np.tile. On décompose ainsi en plusieurs étapes le broadcasting. Ce n'est pas obligatoire mais cela peut aider certains.
np.tilepermet de répliquer un vecteur ou une matrice.
Prenons un exemple :
D = np.array([[1,2],[3,4]])
print(f"D = \n {D} \n")
print("Je réplique D en deux lignes et trois colonnes.")
np.tile(D,(2,3)) # On a ainsi créé une grande matrice en répliquant 2x3 fois le motif 2x2 de départ.
Cette fonction np.tile s'applique aussi à des vecteurs.
print("v1 = \n",v1)
V1 = np.tile(v1,(1,3)) # crée V1 la matrice 4x3 en répliquant v1
print("V1 = \n",V1)
Je vais maintenant construire des matrices V1 et V2 à partir de v1 et v2 en combinant np.newaxis et np.tile.
v1 = np.array([1,3,5,7])
v2 = np.array([2,4,6])
v1 = v1[:,np.newaxis]
v2 = v2[np.newaxis,:]
V1 = np.tile(v1,np.shape(v2)) # croisement avec v2
V2 = np.tile(v2,np.shape(v1)) # croisement avec v1
Notez bien le croisement entre V1 et V2 pour la construction avec np.shape.
Je vérifie les dimensions de V1 et V2:
print("Dimensions de V1 : ", np.shape(V1), " et dimensions de V2 :", np.shape(V2))
et faire la somme : V1 + V2, pour obtenir la même matrice.
V1 + V2
Calcul du développement limité de la fonction exponentielle autour de 0 avec np.tile¶
Prenons le calcul exact de $e^x$ pour 5 valeurs de $x$ comprises entre 0 et 1
n = np.arange(3)
n = n[:,np.newaxis] # Je crée un vecteur colonne de trois valeurs 0,1,2.
x = np.linspace(0,1,5)
x = x[np.newaxis,:] # Je m'assure que x est bien un vecteur ligne (avec 2 dimensions)
# Creation avec np.tile des matrices de travail N et X en croisant les np.shape.
N = np.tile(n,np.shape(x))
X = np.tile(x,np.shape(n))
On dispose maintenant de deux matrices de mêmes dimensions avec lesquelles on peut faire des opérations comme avec des scalaires.
ExpN = X**N/factorial(N) # Avec les matrices X et N, ExpN devient donc très simple à écrire
print(ExpN)
Sur la première ligne de la matrice, on a la fonction 1, la deuxième $x$, la troisième $\frac{x^2}{2!}$.
En utilisant np.sum sur cette matrice, on obtient le résultat cherché et on peut le comparer au résultat exact.
print('Dev Limité de Exp pour x = ',x)
print(np.sum(ExpN,0))
print("à comparer au calcul exact")
print(np.exp(x))