Un estimateur Monte Carlo converge assez lentement comme discuté dans Monte Carlo, convergence et réduction de variance. en pratique, Monte Carlo converge moins vite qu'une intégration par rectangle ou par trapèze (dans certains cas) ...
Voila une comparaison sur la même fonction \( \cos x \) que dans intégration numérique et Monte Carlo : 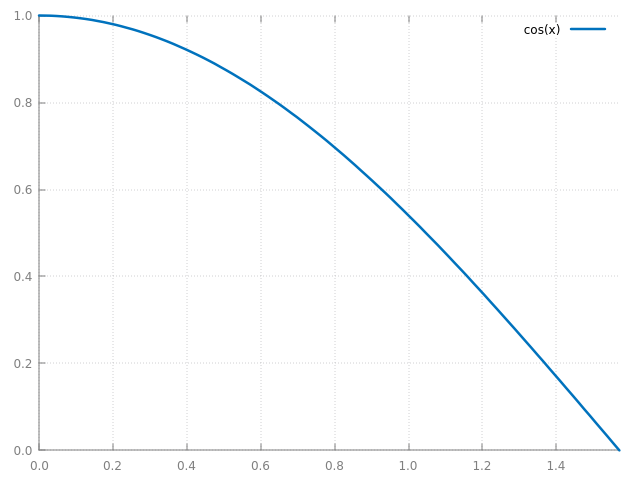
\[ \int_{a=\, 0}^{b= \, 90°} \cos x \, dx \]
On compare l'erreur de l'intégration par rectangle :
\[ \int_a^b \cos x \, dx \approx \sum_i^N \frac{b-a}{N} \, \cos x_i\\ \mbox{avec } x_i= a + \frac{i +\frac{1}{2}}{N} \cdot (b-a) \]
et un estimateur Monte Carlo :
\[ \int_a^b \cos x \, dx \approx \sum_i^N \frac{b-a}{N} \, \cos x_i\\ \mbox{avec } x_i= a + u_i \cdot (b-a)\\ \mbox{ et } u_i \in [0 \, 1) \]
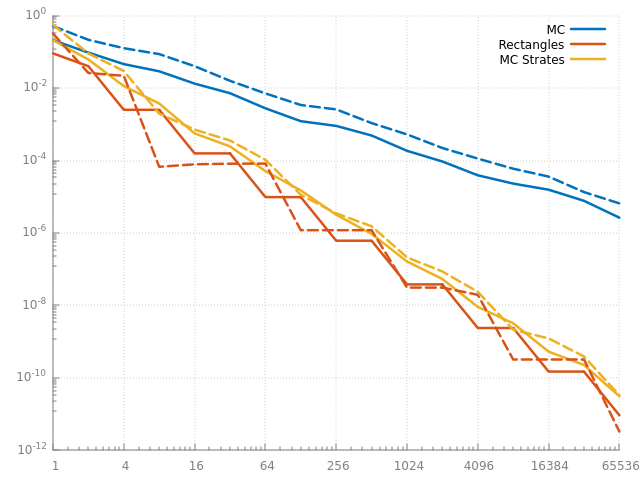
avec 1 échantillon ou 1 rectangle jusqu'à plus de 60000 :
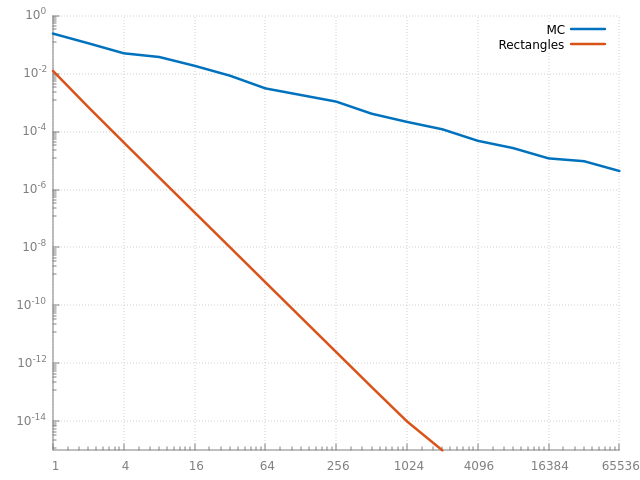
sur cette fonction très simple, l'estimateur ne marche vraiment pas très bien comparé à la méthode des rectangles... ie pour n calculs l'intégration par rectangle est bien plus précise.
d'un coté, on utilise des points parfaitement aléatoires, de l'autre des points parfaitement alignés sur une grille de N intervalles... peut être que l'on peut trouver un hybride intéressant... par exemple, si on utilise des points stratifiés, en génèrant un point aléatoire dans chaque intervalle (au lieu de prendre le centre) :
\[ \int_a^b \cos x \, dx \approx \sum_i^N \frac{b-a}{N} \, \cos x_i\\ \mbox{avec } x_i= a + \frac{i +u_i}{N} \cdot (b-a)\\ \mbox{ et } u_i \in [0 \, 1) \]
qu'est ce qui change ?
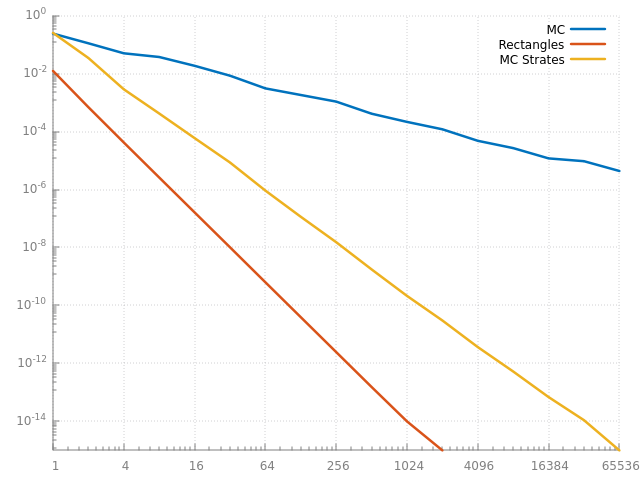
ah ? c'est mieux non ?
pour des fonctions un peu moins simples, comme celles-ci :
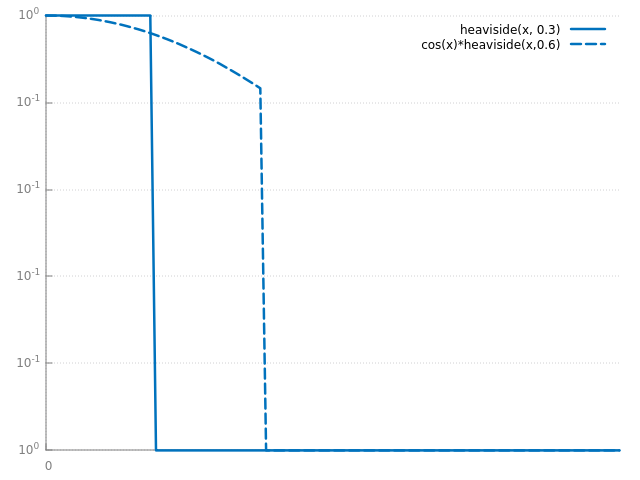
le constat est le même (même si les courbes sont un peu empilées) les points stratifiés fournissent un résultat plus précis que l'estimateur avec des points parfaitement aléatoires.
et sur des fonctions moins simples, l'estimateur Monte Carlo avec des points stratifiés fait presque aussi bien que l'intégration par rectangle ! en pratique, c'est même mieux, puisque l'erreur diminue constamment, ce qui n'est pas toujours le cas avec les rectangles (cf les plateaux des courbes oranges). il faut aussi se rendre compte que ces fonctions sont, assez bizaremment, nettement plus difficiles à intégrer pour les 2 méthodes. vous pouvez regarder les erreurs d'intégration à 1024 points par exemple. la fonction simple a une erreur de \( 10^{-14}\) pour l'intégration par rectangle, alors que les fonctions moins simples ont une erreur de \( 10^{-7}\) environ.
il existe un théorème, cf théorème de Koksma–Hlawka. qui permet de borner l'erreur, la précision, de l'intégration Monte Carlo en fonction de 2 termes : le premier décrit les points utilisés pour intégrer et le deuxième décrit la complexité de la fonction.
Quand on intégre une fonction, on veut utiliser des points avec la plus petite discrépance possible... ce qui permet de réduire l'erreur, d'après le théorème. par exemple, les point aléatoires sont assez mal répartis dans le domaine d'intégration : il y a des "trous", des zones avec peu de points et des "paquets", des zones avec des points très proches les uns des autres, la discrépance est assez importante. Les points stratifiés sont mieux répartis : on a forcé un point par intervalle / rectangle, résultat : les trous sont moins nombreux et plus petits et la discrépance est plus faible que celle des points aléatoires.
Plus les points sont répartis uniformément dans le domaine d'intégration plus la discrépance est petite et meilleure est l'estimation de l'intégrale. La discrépance mesure la différence max entre le nombre de points qui devrait se trouver dans chaque région du domaine et leur nombre réel. Des points parfaits ont une discrépance nulle, mais on ne sait pas construire de tels points. par contre, on sait constuire en 1d ou plus, des points à basse discrépance, ie avec une discrépance plus petite que les points stratifiés des exemples précédents et vraiment plus uniformes que les points aléatoires.
exemples en 2d / histogrammes
stratification et dimension
stratifier des points, c'est facile : on découpe le domaine d'intégration en "rectangles" et on place un point aléatoirement dans chaque rectangle. mais on retombe sur le même problème que l'intégration par rectangle : passé quelques dimensions, il y a beaucoup trop de rectangles !! par exemple, pour calculer une image avec 3 rebonds, le domaine d'intégration fait généralement plus de 20 dimensions ! construire 2 rectangles par dimension représente déjà \( 2^{20}\) rectangles et plus d'un million de points à placer et à stocker.
Avec plusieurs dimensions, c'est déjà plus compliqué, il faut construire des points bien répartis sur chaque axe mais aussi dans tout le domaine. une solution que l'on va pouvoir généraliser par la suite, commence par construire une permutation des N premiers entiers. Il faudra ensuite construire d'autres permutations, une par dimension du domaine tout en garantissant que les points sont en même temps bien répartis sur toutes les dimensions du domaine.
on peut représenter explicitement un entier \( a \) comme un polynome en base \( b \) avec \( n \) chiffres notés \( { a_i } \) :
\[ a= \sum_{i= 0}^{n-1} a_i \cdot b^i \]
et on peut aussi échanger les chiffres et les puissances du polynome :
\[ r= \sum_{i= 0}^{n-1} a_i \cdot b^{n-1-i} \]
on appelle \( r \) le radical inverse de \( a \), on peut utiliser les valeurs de \( r \) comme des points stratifiés, il suffit de le normaliser entre 0 et 1 :
\[ R= \frac{r}{b^n} \]
voila les 16 premières valeurs que l'on obtient en base 2 :
on vient juste de construire une permutation des 16 premiers nombres que l'on peut utiliser comme points pour intégrer :

Les méthodes Monte Carlo utilisent beaucoup de nombres aléatoires, on a déjà vu dans Monte Carlo, éclairage direct : structurer le code une manière de les générer et de les utiliser.
La solution proposée dans Monte Carlo, éclairage direct : structurer le code initialise un générateur différent par ligne de l'image à calculer :
ce qui est simple et facile à utiliser mais qui a un gros défaut : l'image calculée sera différente à chaque exécution et l'ordre d'exécution des threads va aussi avoir une influence sur le résultat. si on souhaite produire la même image avec un thread ou plusieurs, il faut au minimum changer l'initialisation des générateurs aléatoires pour la rendre indépendente du temps (et de l'ordonnancement des threads)...
il y a, en gros, 2 organisations possibles : soit on utilise un seul générateur pour produire une seule séquence de nombres aléatoires que l'on répartit sur les pixels de l'image, soit on utilise un générateur et une séquence de nombres aléatoires différente par pixel.
remarque : l'exemple précédent fait encore autre chose : une séquence par ligne, ce qui fonctionne avec les générateurs classiques mais pas avec les autres...
1 séquence pour toute l'image
comment reproduire la même image que celle calculée par un seul thread et un seul générateur ? rappel : on a créé un générateur par ligne pour simplifier la parallélisation du code dans Monte Carlo, éclairage direct : structurer le code. ce n'est pas vraiment nécessaire, mais ça permet de bien accélérer les calculs.
on suppose que chaque pixel utilise N nombres aléatoires dans la séquence de nombres produite par le générateur.