L3 synthèse d'images
2025

à (re-) lire : géométrie, points et vecteurs

Pour faire les calculs de construction d'une image, il va falloir représenter et manipuler des objets en 3d. En général, on représente la surface des objets avec des points 3d posés dans un repère 3d et des triangles, ou d'autres formes simples comme des sphères ou des cubes.

un point avec 3 coordonnées \( (x, y, z) \) décrit une position dans l'espace.

un vecteur avec 3 coordonnées \( (x, y, z) \) décrit une direction dans l'espace, ou la différence entre 2 points, on peut écrire \( \vec{v}= b - a \), ie comment passer du point a au point b, on peut aussi écrire \( \vec{ab}= b - a \).


conséquence, on peut aussi écrire : \( a + \vec{v} = b\), et \( a= b - \vec{v} \) c'est la méme chose qu'avec des nombres :
si \( d= y - x \) alors \( y= x + d \), et aussi \( x= y - d \) !

les vecteurs sont orientés : si \( \vec{v}= b - a \) permet de passer de \( a \) vers \( b \), alors \( -\vec{v} \) permet de passer de \( b \) vers \( a \).


On peut calculer les coordonnées du vecteur en fonction des coordonnées des points :
\[
    \left( v_x= b_x - a_x,  v_y= b_y - a_y,  v_z= b_z - a_z \right)
 \]

produit scalaire

Le produit scalaire de 2 vecteurs permet de projetter un vecteur sur l'autre, ie d'obtenir sa longueur en fonction de la longueur de l'autre. on note le produit avec l'operateur point : \( \vec{u} \cdot \vec{v} \)


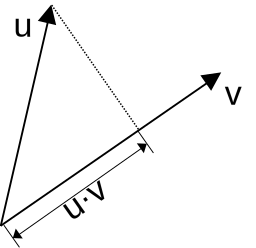
on peut le calculer en fonction des coordonnées des vecteurs :
\[
    \vec{u} \cdot \vec{v}= u_xv_x + u_yv_y + u_zv_z
\]

ou, en fonction de la longueur des vecteurs et du cosinus de leur angle, noté \( \theta \) :
\[
    \vec{u} \cdot \vec{v}= \lVert \vec{u} \rVert  \lVert \vec{v} \rVert \cos \theta
\]

on peut même calculer la longueur d'un vecteur ou la distance entre l'origine et l'extrémité du vecteur : \( \lVert \vec{v} \rVert ^2 = \vec{v} \cdot \vec{v} =  v_x^2 + v_y^2 + v_z^2 \)
ou \( \lVert \vec{v} \rVert = \sqrt{ \vec{v} \cdot \vec{v} } = \sqrt{ v_x^2 + v_y^2 + v_z^2 } \)

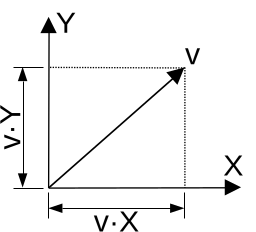
on peut utiliser le produit scalaire pour projetter un vecteur sur les axes d'un repère \( (\vec{X}, \vec{Y}, \vec{Z}) \) et calculer ses coordonnées dans le repère :
\[
    \left( v_x= \vec{v} \cdot \vec{X}, v_y= \vec{v} \cdot \vec{Y}, v_z= \vec{v} \cdot \vec{Z} \right)
 \]



calculs avec un produit scalaire...

comme un produit scalaire s'écrit comme une somme de produit des coordonnées, on peut simplifier pas mal de choses. par exemple :
\[
    \left( t \, \vec{u} \right)  \cdot \vec{v}= t \, \left( \vec{u} \cdot \vec{v} \right) = \vec{u} \cdot \left( t  \, \vec{v} \right)
\]

pourquoi ? il suffit de se rappeller la définition du produit scalaire, et sans trop de surprise, on arrive à écrire : \(  (t \, u_x) \, v_x + (t \, u_y) \, v_y + (t \, u_z) \, v_z = t \, \left( u_xv_x + u_yv_y + u_zv_z \right) \)

et bien sur : \( \vec{u} \cdot \vec{v} = \vec{v} \cdot \vec{u} \)

dans le même genre : le produit scalaire d'une somme de vecteurs : \( \vec{u} \cdot ( \vec{v} + \vec{w} ) = \vec{u} \cdot \vec{v} + \vec{u} \cdot \vec{w} \)

exercice : calculer l'intersection d'un rayon et d'un plan...
on repère un point sur le rayon \( (o, \vec{d}) \) avec une position \( t \) : \( p(t)= o + t \, \vec{d} \).
on connait un point \( a \) ainsi que la normale \( \vec{n} \) du plan.
on utilise une propriété du produit scalaire, 2 vecteurs perpendiculaires ont un produit scalaire nul. ce qui permet d'écrire qu'un point \( p \) dans le plan vérifie : \( \vec{n}  \cdot \vec{ap} = 0 \).

il ne reste plus qu'à écrire la même chose pour un point sur le rayon à une position \( t \) :
\[
\begin{eqnarray*}
\vec{n} \cdot \vec{ap(t)}                 & = & 0\\
\vec{n} \cdot ((o + t \, \vec{d}) - a)             & = & 0\\
\vec{n} \cdot ( \vec{ao} + t \, \vec{d})             & = & 0 \text{ avec } o - a = \vec{ao} \\
\vec{n} \cdot \vec{ao} + \vec{n} \cdot (t \, \vec{d})    & = & 0 \text{ en utilisant la relation } \vec{u} \cdot ( \vec{v} + \vec{w} ) = \vec{u} \cdot \vec{v} + \vec{u} \cdot \vec{w} \\
\vec{n} \cdot \vec{ao} + t \, (\vec{n} \cdot \vec{d})     & = & 0 \text{ avec } \left( t \, \vec{u} \right)  \cdot \vec{v}= t \, \left( \vec{u} \cdot \vec{v} \right) \\
t \, (\vec{n} \cdot \vec{d})     & = & - \vec{n} \cdot \vec{ao}\\
t & = & \frac{ - \vec{n} \cdot \vec{ao} } { \vec{n} \cdot \vec{d} }\\
t & = & \frac{ \vec{n} \cdot \vec{oa} } { \vec{n} \cdot \vec{d} } \text{ avec } \vec{oa} = - \vec{ao}
\end{eqnarray*}
\]

produit vectoriel