Normal Transforms
By Eric Haines (erich@acm.org)  and Tomas Möller (tompa@acm.org) 

A topic rarely covered in computer graphics texts is how surface normals are transformed. In most cases the matrix used to transform a geometric object can also be used to transform the object’s normals. However, it is important to understand when this is not the case. Improperly transforming normals can give incorrect culling and lighting results. Knowing the types of transforms used in your game determines how much care (and additional processing) is needed to properly handle incoming geometry.

Normals must be transformed by the transpose of the inverse of the matrix used to transform geometry¹ (see Turkowski's gem² for a proof and applications in backface culling and shading). So, if the matrix used to transform geometry is called M, then we must use the matrix, N, below to transform the normals of this geometry.

               N = transpose( inverse(M) )

The transpose of a matrix is simply that matrix flipped along its diagonal axis. For example, given the matrix:

the transpose is:

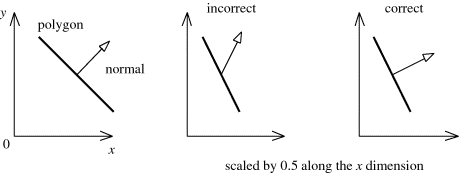
Figure 1 shows what can happen if the proper transform is not used.

Figure 1. On the left is the original geometry, a polygon and its normal shown from the side. The middle illustration what happens if the model is scaled along the x-axis by 0.5 and the normal uses the same matrix. The right figure shows the proper transform of the normal.

In practice, we do not have to compute the inverse if we know the matrix is orthogonal, i.e., that it was formed from only rotations. In this case, the original matrix itself can be used to transform normals, since the inverse of an orthogonal matrix is its transpose. Two matrix transposes cancel out, giving the original rotation matrix. Furthermore, translations do not affect vector direction, so any number of translations can be performed without affecting the normal. After transformation we can also avoid the step of renormalizing the normals (i.e., making their lengths 1 again). This is because length is preserved by a matrix formed with just rotations and translations (such matrices are called rigid-body transforms).

Finally, if a matrix formed by rotations and translations also has only uniform scalings (including uniform reflection matrices) used in forming it, such scalings affect only the length of the transformed normal, not its direction. A uniform scaling is simply a matrix which uniformly increases or decreases the object’s size, vs. a non-uniform scaling, which can stretch or squeeze an object. If uniform scalings are used, then the normals do have to be renormalized. To summarize, if the object is transformed by a matrix consisting of a series of rotations, translations, and uniform scalings, the normal can be safely transformed by this same matrix.

Even if it turns out that the full inverse must be computed, only the transpose of the adjoint of the matrix's upper left 3 x 3 is needed. The adjoint of the matrix is similar to the inverse, except that the matrix computed is not divided by the original matrix's determinant. The adjoint is faster to compute than the inverse. We do not need to divide by the determinant, since we know we generally have to normalize the transformed normal anyway.

It is worth repeating that normal transforms are not an issue in systems where after transformation the surface normal is derived from the triangle (e.g., using the cross product of the triangle's edges). However, it is often the case that triangle vertices contain normal information for lighting, and so normal transformation must be addressed.

Here is code to compute the transpose of the adjoint of a 3 x 3 matrix.

typedef struct ModelMatrix {
          float mtx[3][3];           /* rotation/scale/shear matrix */
                    float translate[3];    /* translation */
} ModelMatrix;

transpose_adjoint( ModelMatrix *m, ModelMatrix *adjoint)
{
/* cofactor for each element */

adjoint->mtx[0][0] = m->mtx[1][1] * m->mtx[2][2] - m->mtx[1][2] * m->mtx[2][1] ;
adjoint->mtx[0][1] = m->mtx[1][2] * m->mtx[2][0] - m->mtx[1][0] * m->mtx[2][2] ;
adjoint->mtx[0][2] = m->mtx[1][0] * m->mtx[2][1] - m->mtx[1][1] * m->mtx[2][0] ;
adjoint->mtx[1][0] = m->mtx[2][1] * m->mtx[0][2] - m->mtx[2][2] * m->mtx[0][1] ;
adjoint->mtx[1][1] = m->mtx[2][2] * m->mtx[0][0] - m->mtx[2][0] * m->mtx[0][2] ;
adjoint->mtx[1][2] = m->mtx[2][0] * m->mtx[0][1] - m->mtx[2][1] * m->mtx[0][0] ;
adjoint->mtx[2][0] = m->mtx[0][1] * m->mtx[1][2] - m->mtx[0][2] * m->mtx[1][1] ;
adjoint->mtx[2][1] = m->mtx[0][2] * m->mtx[1][0] - m->mtx[0][0] * m->mtx[1][2] ;
adjoint->mtx[2][2] = m->mtx[0][0] * m->mtx[1][1] - m->mtx[0][1] * m->mtx[1][0] ;
}

References
1. Hanrahan, Pat, "A Survey of Ray-Surface Intersection Algorithms", chapter 3 in Andrew Glassner (editor), An Introduction to Ray Tracing, Academic Press Inc., London, 1989.
2. Turkowski, Ken, "Properties of Surface-Normal Transformations", in Andrew Glassner (editor), Graphics Gems, Academic Press, Inc., pp. 539-547, 1990. http://www.worldserver.com/turk/computergraphics/index.html