Le TP se programme en C++ en utilisant une base de code
minimaliste qu'il faut installer. cf doc
en ligne.
Il faudra éventuellement vous familiariser avec premake et git,
en plus d'un environnement de développement C++.
La base de code est portable sous linux et windows mais également
mac os.
Si vous ne souhaitez pas utiliser git, vous pouvez néanmoins
récupérer un zip des sources sur le dépot.
Compilez et exécutez tp1.cpp ou tp2.cpp qui se trouvent dans le
dossier projets.
Pour commencer en douceur : comment calculer l'intersection d'un
rayon et d'un plan ? Comment représenter un rayon ? un plan ?
On représente généralement le rayon par son origine, sa direction
et une abscisse (paramétrique) max. Un rayon peut être une
demi-droite infinie ou un segment.
On représente habituellement le plan par un point et une normale. cf les types Point et Vector définis dans vec.h (et vec.cpp)#include "vec.h" // pour Point et Vector
struct Ray
{
Point o; // origine
Vector d; // direction
float tmax; // position de l'extremite, si elle existe. le rayon est un segment / un intervalle [0 tmax]
// le rayon est un segment, on connait origine et extremite, et tmax= 1
Ray( const Point& origine, const Point& extremite ) : o(origine), d( Vector(origine, extremite) ), tmax(1) {}
// le rayon est une demi droite, on connait origine et direction, et tmax= inf
Ray( const Point& origine, const Vector& direction ) : o(origine), d(direction), tmax(FLT_MAX) {}
// renvoie le point sur le rayon pour t
Point point( const float t ) const { return o + t * d; }
};
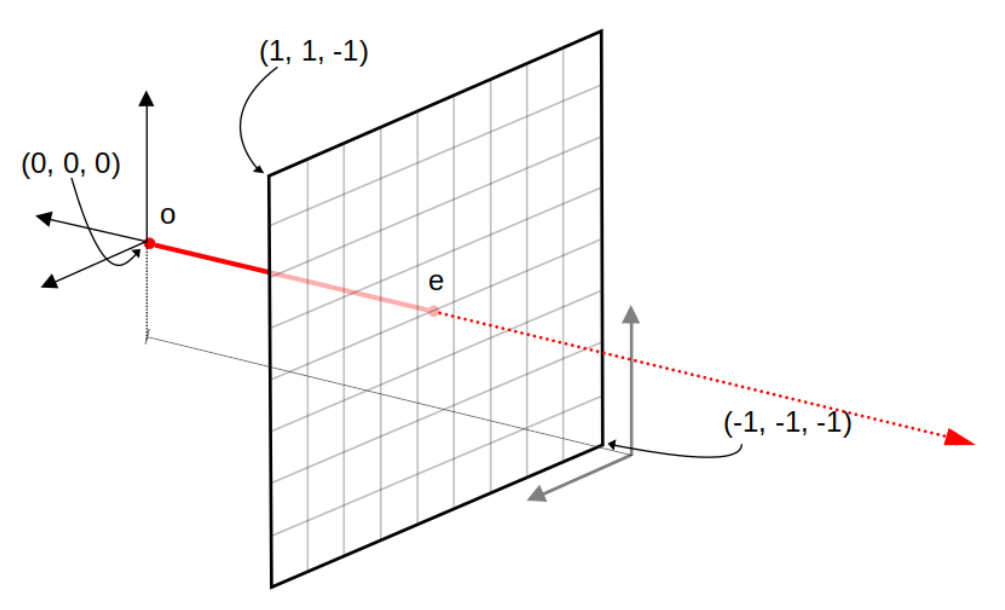
Maintenant que le code de base est fonctionnel, comment décrire une camera et construire les rayons passant par les pixels de l'image ?
rappel : on peut schématiser la construction de l'image par un plan image à z= -1 :

Il ne reste plus qu'à calculer les coordonnées du centre d'un
pixel (x, y) dans le plan image. On connait l'origine du rayon par
construction, c'est le point o et le rayon passe par le point e,
le centre du pixel, ce qui permet de construire sa direction. On
considère que les rayons issus de la camera sont infinis.
Maintenant que l'on sait calculer le rayon d'un pixel, il ne
reste plus qu'à écrire la boucle qui parcours tous les pixels de
l'image. cf doc
de la classe Image. vous pouvez utiliser projets/tp2.cpp comme
code de départ.
Dernière étape, calculer les intersections des objets et des
rayons pour déterminer quel est l'objet visible à travers chaque
pixel.
rappel : on ne s'intéresse qu'à l'intersection valide la
plus proche de l'origine du rayon...
remarque : les objets placés devant la camera ont leur
coordonnée z < 0. On utilise un repère droit / classique pour
le plan image, X vers la droite, Y vers le haut et Z pointe donc
derrière la camera.
Comment distinguer les différents objets ? Le plus simple est de
donner une couleur différente à chaque objet. par exemple : un
plan gris neutre, une sphère rouge et un ciel noir... cf doc
de Color.

struct Hit
{
float t;
Point p;
Vector n;
Color color; // ou Material material; si avez une description de matière plus complète, avec des reflets par exemple...)
};
On suppose qu'un soleil éclaire la sphère. Comment dessiner l'ombre de la sphère ?

les défauts d'intersections se corrigent assez facilement : cf doc
en ligne : "precision
numérique et lancer de rayons"

ce qui permet d'abstraire la représentation de la scène et de la faire évoluer sans modifier son utilisation. ce sera très pratique lorsque l'on regardera comment accélérer les calculs d'intersection rayon / primitives.struct Scene
{
std::vector objets;
Hit intersect( const Ray& ray );
bool visible( const Point& p, const Point& q );
// const Material& material( const Hit& hit ); // renvoie la matiere au point d'intersection
};
intersect()
est adaptée aux rayons infinis comme ceux issus de la camera, la
fonction doit renvoyer l'intersection valide la plus proche de
l'origine du rayon. visible() est utilisée pour vérifier que 2 points se
voient, pour calculer les ombres, par exemple. visible(),
ie ce n'est pas la peine de vérifier qu'une intersection valide est
bien la plus proche de l'origine du rayon... et de compiler en mode Release :Image image(512, 512);
#pragma omp parallel for schedule(dynamic, 1)
for( int py= 0; py < image.height(); py++ )
for( int px= 0; px < image.width(); px++ )
{
Point o= Point(0, 0, 0);
Vector d= { ... };
Ray ray(o, d);
Hit h= scene.intersect(ray);
...
}
make -j4 config=release tp2
On peut aussi prévoir de déplacer la camera ou les objets, en
utilisant une transformation (cf doc
en ligne). On peut aussi généraliser la projection de la camera en
utilisant une transformation perspective ou orthographique,
etc... cf doc.