Convex order and increasing convex order for McKean-Vlasov processes with common noise
Abstract: We establish results on the conditional and standard convex order, as well as the increasing convex order, for two processes $X = (X_t)_{t \in [0, T]}$ and $Y = (Y_t)_{t \in [0, T]}$, defined by the following McKean-Vlasov equations with common Brownian noise $B^0 = (B_t^0)_{t \in [0, T]}$:
$$\displaystyle \begin{align} dX_t &= b(t, X_t, \mathcal{L}^1(X_t))dt + \sigma(t, X_t, \mathcal{L}^1(X_t))dB_t + \sigma^0(t, \mathcal{L}^1(X_t))dB^0_t, \nonumber \\ dY_t &= \beta(t, Y_t, \mathcal{L}^1(Y_t))dt + \theta(t, Y_t, \mathcal{L}^1(Y_t))dB_t + \theta^0(t, \mathcal{L}^1(Y_t))dB^0_t, \nonumber \end{align} $$where $\mathcal{L}^1(X_t)$ (respectively $\mathcal{L}^1(Y_t)$) denotes a version of the conditional distribution of $X_t$ (resp. $Y_t$) given $B^0$. These results extend those established for standard McKean-Vlasov equations in Liu et al. (2023) and Liu and Qiu (2021). Under suitable conditions, for a (non-decreasing) convex functional $F$ on the path space with polynomial growth, we show $\mathbb{E}[F(X) \mid B^0] \leq \mathbb{E}[F(Y) \mid B^0]$ almost surely. Moreover, for a (non-decreasing) convex functional $G$ defined on the product space of paths and their marginal distributions, we establish
$$\displaystyle \begin{align} \mathbb{E}\Big[G\big(X, (\mathcal{L}^1(X_t))_{t\in[0, T]}\big)\Big| B^0\Big] \leq \mathbb{E}\Big[G\big(Y, (\mathcal{L}^1(Y_t))_{t\in[0, T]}\big)\Big| B^0\Big] \quad \text{a.s.} \nonumber \end{align} $$Similar convex order results are also established for the corresponding particle system. Finally, we explore applications of these results to stochastic control problems—deducing in particular an associated comparison principle for Hamilton-Jacobi-Bellman equations with different coefficients—and to the interbank systemic risk model introduced by Carmona, Fouque, and Sun (2015).
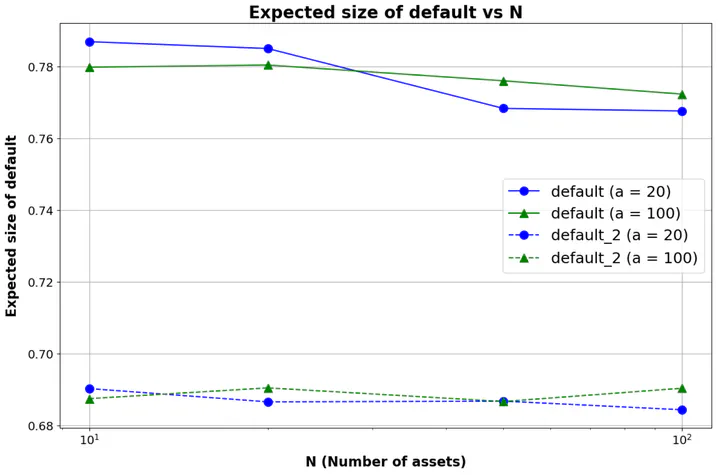
What’s the graph about ? On the figure, one can see the expected size of default in a systemic risk model for interbank exchanges. This is a convex functional. On the top, the processes have diffusion coefficients $\sigma = 4$ and common diffusion coefficient $\sigma^0 = 3$. On the bottom, the processes $(X^i)_{1 \le i \le N}$ have a diffusion coefficients $\theta(X^i) = 4 S(X^i)$ where $S$ is the sigmoid function, so that $\theta \le \sigma$, and common diffusion coefficient $\theta^0 = 2 \le \sigma^0$. As predicted by our result on the convex order for particle system, the expected size of default of the second model is consistently below the one of the first.
About my co-authors: You can find Yating’s webpage here and Théophile’s info here.