Mean-field approximation, Gibbs relaxation, and cross estimates
While it is known that propagation of chaos holds at rate $O(1/N)$ uniformly in time, and Gibbs relaxation at rate $O(e^{-ct})$ uniformly in $N$, we go a step further by showing that the cross error between chaos propagation and Gibbs relaxation is $O(N^{-1}e^{-ct})$.
Jul 31, 2025
Convex order and increasing convex order for McKean-Vlasov processes with common noise
We establish the conditional convex order and increasing convex order for McKean-Vlasov equations with common noise. Applications to stochastic control are also discussed.
Apr 24, 2025
Creation of chaos for interacting Brownian particles
We establish a fine version of the so-called creation-of-chaos phenomenon':' in weak norms, the mean-field approximation for a typical particle is shown to hold with an accuracy O(1/N) up to an error due solely to initial pair correlations.
Apr 14, 2025
Particle method for the numerical simulation of the path-dependent McKean-Vlasov equation
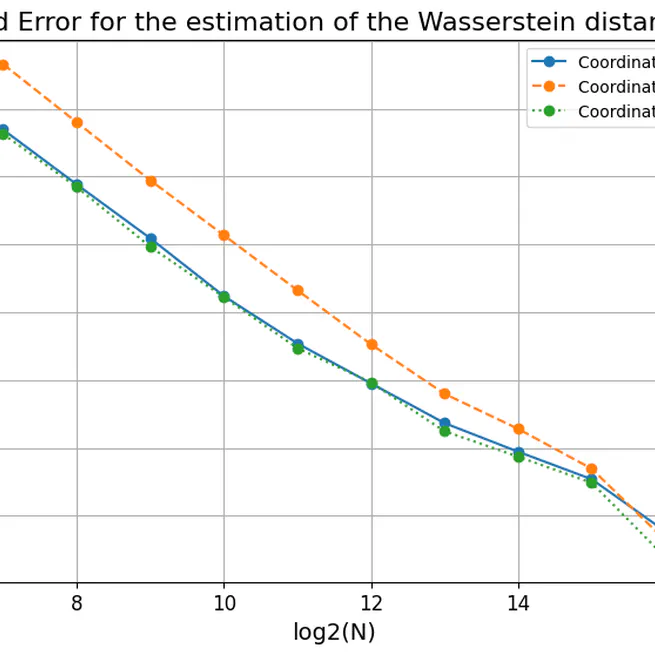
We present the particle method for simulating the solution to the path-dependent McKean-Vlasov equation.
Jun 1, 2024
Homogenization of Active Suspensions and Reduction of Effective Viscosity
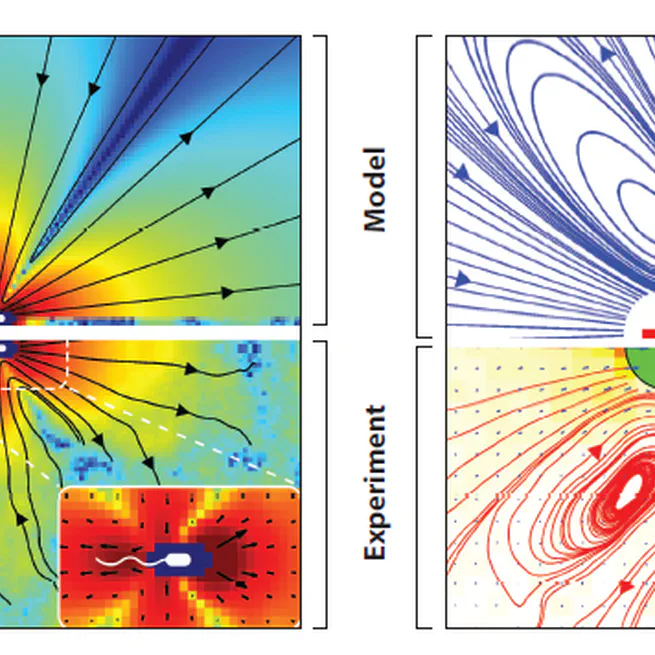
We consider a suspension of active rigid particles (swimmers) in a steady Stokes flow, using for simplicity a steady-state model where particles are distributed according to a stationary ergodic random process, and we study its homogenization in the macroscopic limit. An analysis in the dilute regime shows that the activity of the particles can either increase or decrease the effective viscosity (depending on the swimming mechanism), in a way that strongly differs from the well-known effect of passive suspensions.
Mar 1, 2023