Notes sur le cours de codage, transmission, compression
Ce cours présente tout ce qu'il est nécessaire de savoir pour comprendre comment fonctionne la transmission de grosses données via le réseau :
- Le codage : du bit aux entiers jusqu'aux images.
- La théorie de l'information.
- La compression : compression de données quelconques et de signaux.
- La transmission fait partie intégrante du cours car elle influe les méthodes de codage et les algorithmes de compression.
Les points fondamentaux de ce cours :
- Un signal est une donnée particulière car bruitée.
- On doit tenir compte de l'utilisateur de la donnée.
- Compresser, c'est modéliser.
- On normalise le DÉcompresseur.
- On doit tenir compte du mode d'accès à la donnée compressée.
Plan du cours
- Notes sur le cours de codage, transmission, compression
- Codage
- L'équilibrage de probabilités
- Compression de données
- Compression de signal
- Formats de fichiers
- Divers
Codage
On décrit ici, le codage des principaux types de base. Un bon codage permet d'utiliser moins de place et est plus rapidement compressable.
Le bit
- Le mot bit désigne deux choses qui n'ont rien à voir :
- Le bit est l'unité de mesure de la quantité d'information.
- Le bit est la quantité d'information minimale que l'on peut stocker physiquement dans la mémoire de l'ordinateur.
Le deuxième porte ce nom car il peut contenir jusqu'à 1 bit d'information, mais il peut en contenir moins (c'est pourquoi l'on a besoin de faire de l'équilibrage de probabilités).
Il est théoriquement possible de faire des mémoires dont l'élément de base permettrait de stocker plus d'un bit d'information. Mais les opérations réalisées serait plus complexe que la logique booléenne : http://www.cs.berkeley.edu/~randy/CLD/CLD.html
L'entier positif
Un entier positif peut-être écrit en base 2 (binaire), en peut donc le stocker en machine sous la forme d'une suite de bits de longueur variable
0() 1(1) 2(10) 3(11) 4(100) 5(101)
La valeur de l'entier : \(... + 8*b_3 + 4*b_2 + 2*b_1 + b_0\)
Le codage simple des entiers
Le stockage le plus simple consiste à stocker des entiers contenant un nombre fixé de bits : 8 (octet), 16, 32, 64 bits. Cela fait perdre de la place mais permet d'avoir un accès aléatoire rapide. On appelle mot (word) l'entier pour lequel le CPU travaille le plus naturellement (souvent la largeur du bus de donnée).
Conversion entier en binaire
Une fonction utilitaire implémentée de 3 manières différentes :
int est_impair(int entier) { return entier - 2*(entier/2) ; // Si division entiere return entier % 2 ; // % = le modulo return entier & 1 ; // ET BINAIRE du langage C }
Affiche un entier sous la forme d'une suite de bits du poids fort au poids faible. Attention, le nombre 0 est une suite vide.
void affiche_entier_en_binaire(int entier) { if (entier) { affiche_entier_en_binaire(entier / 2) ; if (est_impair(entier)) affiche('1') ; else affiche('0') ; } }
Affichage d'un entier en décimal.
void affiche_entier_en_decimal(int entier) { if (entier) { affiche_entier_en_decimal(entier / 10) ; affiche( '0' + entier % 10 ) ; } }
Convertion d'une chaine de caractères contenant des chiffres en un entier :
int decimal_en_entier(char *chaine) { int entier = 0 ; while( *chaine ) entier = 10 * entier + (*chaine++ - '0') ; return entier ; }
Question : si l'on a une machine qui stocke l'information sur des trit (au lieu de 2 valeurs on en a 3). Les programmes précédents vont-ils fonctionner ?
Les codages décimal en binaire
Dans les débuts de l'informatique, les temps de conversion entre le format binaire et un affichage décimal prenait du temps (division et multiplications) pour éviter cela on travaillait en BCD (Binary Coded Decimal).
Un chiffre décimal est codé sur 4bit, les valeurs 10 à 15 sont perdues.
EBCDIC (Extended Binary Coded Decimal Interchange Code) était une extension à 8 bits (non portable d'un pays à l'autre).
Les entiers codés sur plus d'un octet
L'ordre naturel de codage des bits du plus fort au plus faible n'est pas forcement respecté. Sur X86, le codage sur 2 octets est :
- 7,6,5,4,3,2,1,0
- 15,14,13,12,11,10,9,8
Cette ordre permet au processeur dont le mot est l'octet de faire des additions sur plusieurs octets en lisant la mémoire du début à la fin. Ce permet d'obtenir un débit maximum car la mémoire RAM est optimisée pour ce cas de figure.
La plupart des algorithmes seraient beaucoup plus naturels si les nombres étaient écrits du poids faible au poids fort. Y compris dans la vie courante, en effet on est obligé de compter le nombre de chiffres avant de pouvoir commencer à prononcer un nombre. Il faut remarquer que ce sont des chiffres arabes, et que pour eux, on écrit bien les unités en premier, ce qui est bien plus logique.
Codage redondant
Le codage redondant s'appelle ainsi car un même entier peut s'écrire de différentes façons.
Le codage redondant permet d'accélérer les calculs au détriment de la place mémoire occupée. En effet, le parallèlisme ne peut être utilisé pour faire une addition à cause de la retenue. Classiquement pour calculer \(a_2 a_1 a_0 + b_2 b_1 b_0\) on fait les opérations suivantes :
- \(a_0 + b_0\) et \(r_0\) la retenue.
- Puis \(a_1 + b_1 + r_0\) et \(r_1\) la retenue.
- Puis \(a_2 + b_2 + r_1\) et \(r_2\) le débordement.
En notation redondante, chaque bit est doublé, le deuxième bit contient la retenue de la précédente opération effectuée. L'addition se fait en une seule étape avec 3 calculs en parallèle :
- \(a_2 + b_2 + r_1\) et \(r_2\) le débordement.
- \(a_1 + b_1 + r_0\) et \(r_1\) la retenue.
- \(a_0 + b_0\) et \(r_0\) la retenue,
Avec cette méthode, l'addition de deux entier de 32 bits prend 31 fois moins de temps. Par contre pour stocker le résultat en mémoire centrale, il faut enlever la redondance ce qui est long car on doit faire remonter le bit de retenu.
Codes de Gray (1953)
Une manière d'énumérer les entiers qui assure de n'avoir qu'un chiffre différent entre deux entiers énumérés l'un après l'autre. En décimal : 0 1...8 9 19 18...11 10 20 21...28 29 39 38...91 90 190 191...
L'application principale est pour les capteurs de position. En effet, quand on se trouve dans un cas limite, on ne peut se tromper que de 1 alors qu'avec l'énumération classique on peut obtenir 199, 109, 190, 0, 9, 90 quand on est entre 99 et 100.
Soit le capteur linéaire suivant avec 4 récepteurs binaires :
0123456789ABCDEF
Bit 0 .##..##..##..##.
Bit 1 ..####....####..
Bit 2 ....########....
Bit 3 ........########
^
La position décodée est 7
On peut faire des capteurs de rotations. Dans ce cas on met les poids faibles à l'extérieur du cercle pour les agrandir le plus possible.
Entier négatif
Le but est coder les entiers négatif de telle façon que les opérations fonctionnant sur les entiers positifs fonctionnent aussi sur les entiers négatifs sans modification.
Complément à 1 : Inverser la valeur des chacun des bits de l'entier.
Complément à 2 : Faire le complément à 1 et ajouter 1
Si l'on dispose de \(n\) bits, on code directement les entier positifs de \(0\) à \(2^{n-1} - 1\). Pour les négatifs, on applique le complément à 2 de sa valeur absolu, on peut coder de \(-2^{n-1}\) à \(-1\).
| Entier | Codage | Complément à 1 | Complément à 2 |
|---|---|---|---|
| -4 | 100 | ||
| -3 | 101 | ||
| -2 | 110 | ||
| -1 | 111 | ||
| 0 | 000 | 111 | 000 |
| 1 | 001 | 110 | 111 |
| 2 | 010 | 101 | 110 |
| 3 | 011 | 100 | 101 |
| 4 | 011 | 100 |
Il est tout de même nécessaire d'ajouter un indicateur de débordement de l'avant-dernier bit afin de savoir s'il y a eu un débordement. Attention, en langage C :
- on n'est pas prévenu de ce fait.
- la norme indique explicitement qu'en cas de débordement le résultat peut être n'importe quoi.
Un exemple du monde réel (noyau linux) :
int a, b ; // des valeurs quelconques if ( a>0 && b>0 ) if ( a + b < 0 ) La somme de deux nombres positifs est un nombre positif. donc le compilateur a le droit d'enlever ce test.
Pointeur
Un pointeur est un entier permettant de retrouver une information en mémoire. Le pointeur est un indice dans un tableau d'élément commençant au début de la mémoire.
De nos jours les pointeurs indicent des tableaux d'octets. Le pointeur sur une donnée de base (entier, flottant) doit souvent être multiple de la taille de la donnée.
- Avantage : Uniformité.
- Inconvénients :
- perte d'espace adressable,
- impossibilité d'adresser le bit.
- codage de pointeurs invalides : la donnée est à cheval sur deux mots mémoire. Ces pointeurs sont invalides ou bien ralentissent le processeur.
Les pointeurs retournés par malloc sont utilisables pour stocker un table de double, il faut donc qu'ils soient un multiple de sizeof(double).
Remarque concernant l'interpréteur LISP. Quelque bits du pointeur sont utilisés pour indiquer le type de l'objet pointé (entier, caractère, chaine, objet...).
Codage de quadtree/octree
Les pointeurs prennent beaucoup de place, 32 ou 64 bits sur les machines actuelles. Et des structures de données comportent principalement des pointeurs, par exemple les quadtree, octree...
Si chaque objet :
- est accessible que par un pointeur unique ;
- est de même taille que tous les autres.
on peut alors drastiquement diminuer la taille des pointeurs de la manière suivante :
- On calcule une clef de hashage à partir de l'adresse précise ou est stockée le pointeur lui-même.
- Cette clef permet d'accéder à l'objet dans la table de hashage
- Pour résoudre les conflits, on peut stocker à l'emplacement du pointeur un décalage dans la table de hashage ou bien indiquer le code d'une autre fonction de hashage.
Avec une telle méthode et une table de hashage de taille raisonnable, on peut stocker seulement 3 bits par pointeur. Cela nécessite bien sûr que l'on va stocker plusieurs pointeurs à l'intérieur d'un entier et que les adresses des pointeurs sont des adresses de bit et non d'octet.
Virgule fixe
Le nombre de chiffres (en base 2) après la virgule est constant : \(v\). On se contente donc de multiplier le nombre par \(2^v\) et de le coder comme un entier.
Cela ne change rien aux opérations habituelles, on réutilise donc toute les opérations entières. Mais attention, il faut renormaliser après les multpiplications et divisions.
On code 6.625 avec 4 bits après la virgule comme 110 1010
Diviseur vaut 2 puissance le nombre de bits après la virgule. La fonction suivante se termine toujours, pourquoi ?
int affiche_entier<1_decimal(int entier, int diviseur) { if (entier) { entier = entier * 10 ; affiche( '0' + entier/diviseur ) ; affiche_entier<1_decimal(entier % diviseur, diviseur) ; } }
Combien de bits après la virgule pour coder 0.3 ?
float a ; a = 0.3 ; if ( a != 0.3 ) printf("Programme faux\n") ;
Virgule flottante
Toujours se rappeler que virgule flottante ne signifie pas nombre réel, on ne peut pas coder les réels en machine (sauf exceptions rarissimes)
Un nombre flottant peut s'écrire sous la forme normalisée : \(mantisse * 2^{exposant}\) avec \(2 > mantisse >= 1\)
- On code l'exposant comme un entier biaisé et non signé. Pour un exposant si 8 bits, on code l'exposant \(3\) comme \(127+3 = 130\). Cela permet de simplifier les comparaisons et de choisir éventuellement d'autoriser plus de grandes puissances que de petites.
- La mantisse est codée comme en entier positif, auquel on enlève le premier bit (toujours égal à 1).
On code donc :
- le signe de la mantisse (0:positif)
- l'exposant + X
- la mantisse sans le premier bit
Pour un flottant simple (32 bits), 1 bit de signe, 8 bits d'exposant (-128...127) et 23 bits de mantisse :
| Exposant | Mantisse | Valeur |
|---|---|---|
| 127 | != 0 | NaN |
| 127 | == 0 | \(\pm \infty\) |
| -128 | == 0 | \(\pm 0\) |
| -128 | != 0 |
|
| >-128 & <127 | \(\pm (1 \circ mantisse) * 2^{exposant}\) |
Le résultat de la comparaison de deux flottants est le même que celui des deux représentations vu comme des entiers.
Caractères
ASCII 7 et 8 bits
Première norme : ASCII 7 bits (American Standard Coding for Information Interchange). Le bit de poids fort sert de controle de parité. Elle permet de coder 128 caractères avec 33 caractères de contrôle.
L'ASCII 8 bits offre des caractères supplémentaires adaptés à la langue. Il y a plusieurs ASCII 8 bits standardisés :
ISO 8859-1 West European languages (Latin-1) ISO 8859-2 Central and East European languages (Latin-2) ISO 8859-3 Southeast European and miscellaneous languages (Latin-3) ISO 8859-4 Scandinavian/Baltic languages (Latin-4) ISO 8859-5 Latin/Cyrillic ISO 8859-6 Latin/Arabic ISO 8859-7 Latin/Greek ISO 8859-8 Latin/Hebrew ISO 8859-9 Latin-1 modification for Turkish (Latin-5) ISO 8859-10 Lappish/Nordic/Eskimo languages (Latin-6) ISO 8859-11 Latin/Thai ISO 8859-13 Baltic Rim languages (Latin-7) ISO 8859-14 Celtic (Latin-8) ISO 8859-15 West European languages (Latin-9) ISO 8859-16 Romanian (Latin-10)
Astuces sous Unix :
- la variable LC_CTYPE=fr_FR.utf8 définie les classes de caractère (minuscule/majuscule/...)
- LC_COLLATE définie comment on les trie (cas du ss en espagnol qui utilise les mêmes caractères que le français). Attention l'ordre alphabétique n'est pas standardisé.
- Pour connaître votre environnement, la commande est locale
- Pour découvrir les typographies : gnome-character-map
Le tableau 16x16 suivant le latin1 (ISO-8859-1) donc sans le symbole € ni le œ lié. Le code du caractère est 16 fois la colonne plus la ligne.
+ 0 1 2 3 4 5 6 7 8 9 A B C D E F
0 NUL ^@ DLE ^P 0 @ P ` p 0x80 0x90 ° À Ð à ð
1 SOH ^A DC1 ^Q ! 1 A Q a q 0x81 0x91 ¡ ± Á Ñ á ñ
2 STX ^B DC2 ^R " 2 B R b r 0x82 0x92 ¢ ² Â Ò â ò
3 ETX ^C DC3 ^S # 3 C S c s 0x83 0x93 £ ³ Ã Ó ã ó
4 EOT ^D DC4 ^T $ 4 D T d t 0x84 0x94 ¤ ´ Ä Ô ä ô
5 ENQ ^E NAK ^U % 5 E U e u 0x85 0x95 ¥ µ Å Õ å õ
6 ACK ^F SYN ^V & 6 F V f v 0x86 0x96 ¦ ¶ Æ Ö æ ö
7 BEL ^G \a ETB ^W ' 7 G W g w 0x87 0x97 § · Ç × ç ÷
8 BS ^H \b CAN ^X ( 8 H X h x 0x88 0x98 ¨ ¸ È Ø è ø
9 HT ^I \t EM ^Y ) 9 I Y i y 0x89 0x99 © ¹ É Ù é ù
A LF ^J \n SUB ^Z * : J Z j z 0x8a 0x9a ª º Ê Ú ê ú
B VT ^K ESC ^[ + ; K [ k { 0x8b 0x9b « » Ë Û ë û
C FF ^L \f FS ^\ , < L \ l | 0x8c 0x9c ¬ ¼ Ì Ü ì ü
D CR ^M \r GS ^] - = M ] m } 0x8d 0x9d ½ Í Ý í ý
E SO ^N RS ^^ . > N ^ n ~ 0x8e 0x9e ® ¾ Î Þ î þ
F SI ^O US ^_ / ? O _ o DEL 0x8f 0x9f ¯ ¿ Ï ß ï ÿ
Attention 0xA0 est l'espace insécable donc non visible, certain caractères peuvent ne pas s'afficher sur votre navigateur web.
Unicode
- Une table de caractères sur 16 bits (pour les langues vivantes) permettant de coder tous les caractères utilisés.
- Les 256 premiers codes sont l'ISO8859.1.
- Les codes sont unifiés (le caractère A n'apparait qu'une fois) sauf pour les caractères composés (e + ´ = é).
- Ils ne représentent pas un graphisme associé à la lettre (italique/gras/...) sauf dans des cas comme minuscule/majuscule ou début/milieu/fin de mot.
- Des caractères de contrôle permettent la composition ou d'ajouter des attributs modificateurs de graphisme ou de sens d'écriture.
UTF-8
C'est un codage de l'Unicode (jusqu'à 31 bits par caractère dans la version initiale, mais maintenant restreint à 21 bits pour être compatible avec l'UTF16).
0x00000000 - 0x0000007F: 7 bits
0xxxxxxx
0x00000080 - 0x000007FF: 11 bits
110xxxxx 10xxxxxx
0x00000800 - 0x0000FFFF: 16 bits
1110xxxx 10xxxxxx 10xxxxxx
0x00010000 - 0x001FFFFF: 21 bits
11110xxx 10xxxxxx 10xxxxxx 10xxxxxx
0x00200000 - 0x03FFFFFF: 26 bits
111110xx 10xxxxxx 10xxxxxx 10xxxxxx 10xxxxxx
0x04000000 - 0x7FFFFFFF: 31 bits
1111110x 10xxxxxx 10xxxxxx 10xxxxxx 10xxxxxx 10xxxxxx
Avantages :
- Totalement compatible avec les logiciels existant qui travaillent en ASCII 7bits, par exemple le système d'exploitation. (Pas de problème pour le '/' et NULL).
- Codage redondant donc détection d'erreur possible ou détection automatique du codage.
Problèmes :
- accès aléatoire impossible (est-ce utile ? car le réalignement est possible grace à la redondance),
- perte de 50% de place dans le cas des caractères entre 4096 et 65536 mais cela ne doit pas gêner les ISO8859 qui sont tous entre 0 et 4096.
- Un caractère peut avoir plusieurs codage, seul le plus court est valide. C'est pour éviter des trous de sécurité comme le /.. dans les serveurs web.
Le BOM (Byte Order Mark) indique si l'on est little ou big endian. C'est 0xEF 0xBB 0xBF pour indiquer big endian qui correspond au caractère U+FEFF (ZERO WIDTH NO-BREAK SPACE)
Chaîne de caractères
Deux méthodes pour les coder :
- Le début de la chaîne contient la longueur (Pascal), l'inconvénient est que la chaîne a une longueur limité à moins d'utiliser un entier de longueur variable. Un autre inconvénient est que l'on ne peut pas passer la suite d'une chaine sans détruire le début.
- Un caractère de fin de chaîne existe, l'inconvénient est que l'on ne peut le coder dans la chaîne (à moins de faire un code d'échappement)
Codage des dates
La méthode la plus simple est de coder la date comme un nombre d'unités (..., secondes, minutes, heures, ...) depuis une date de base. Cette méthode est la plus compacte, permet des opérations aisées, est indépendante du calendrier à tous points de vue. Le seul inconvénient est la traduction de l'un à l'autre. (changement de calendrier cal 1752 ou minutes de 62 secondes)
Codage d'arbre binaire
Utile pour la suite du cours. Le codage est simple, il suffit d'ajouter un bit à 0 devant l'information concernant les noeuds et 1 devant l'information concernant les feuilles. Cela donne (en simplifiant) :
0 infos noeud 1 infos feuille 0 infos noeud 1 infos feuille 1 infos feuille
affiche(Arbre *a) { if ( noeud(a) ) { affiche_bit(0) ; affiche_infos_noeud(a) ; affiche(a->gauche) ; affiche(a->droite) ; } else { affiche_bit(1) ; affiche_infos_feuille(a) ; } } Arbre * lecture() { if ( lit_bit() ) return creer_feuille( lit_infos_feuille() ) ; else // Ce qui suit est faux. Pourquoi ? return creer_noeud(lit_infos_noeud(), lecture(), lecture()) ; }
Codage d'arbre quelconque
Très simple :
- Un bit à 0 indique la fin de codage d'un sous-arbre.
- Un bit à 1 est suivi de l'information associée au noeud, suivi du codage du premier fils, suivi du codage du frère suivant.
- On ne fait pas la différence entre une feuille et un noeud sans fils.
Exemple :
- : 0
- A : 1 A 0 0
- A B C D E : 1A0 1B0 1C0 1D0 1E0 0
- A(B C D E) : 1A 1B0 1C0 1D0 1E0 0 0
- A(B C D) E : 1A 1B0 1C0 1D0 0 1E0 0
- A(B(C(D(E)))) : 1A 1B 1C 1D 1E0 0 0 0 0 0
Codes détecteur/correcteurs d'erreur
Ce sont des codages permettant de détecter et/ou corriger des erreurs de transmission de données.
Codes linéaires
Ce sont des codes redondants. C'est-à-dire que l'information est stockée avec plus de bits qu'il n'en faut, mais que si l'un des bits (ou plusieurs) est modifié, sa valeur initiale peut être inférée. C'est un domaine très complexe. Voici une simplification pour vous faire comprendre.
Si l'on représente graphiquement les entiers transmis dans un espace de dimension \(n\) (nombre de bits). Il peut y avoir détection d'une erreur si la modification d'un bit d'un entier ne le transforme pas en un autre. Il peut y avoir correction si la modification de 2 bits ne le transforme pas en un autre. Pour cela on calcule la distance entre entiers qui est le nombre de bits différents : c'est la distance de Hamming.
| Distance | Détecte bit faux | Correction bit faux |
|---|---|---|
| 1 | 0 | 0 |
| 2 | 1 | 0 |
| 3 | 1 | 1 |
| 4 | 2 | 1 |
| 5 | 2 | 2 |
Exemple de distance sur des entiers :
| Nom | Ensemble d'entier | Distance entre-eux | Distance à 0 |
|---|---|---|---|
| A | 1 1 1 1 | 0 | 1 |
| B | 1000 0100 0010 0001 | 2 | 1 |
| C | Entiers avec au moins 1 bit à 1 | 1 | 1 |
| D | Entiers avec 2 bits à 1. Si \(k\) bits, il y en a \(2^k - k - 1\) |
1 | 2 |
| E | B A | 2 | 2 |
| F | B D | 3 | 3 |
On peut représenter le codage par un produit matrice vecteur ou l'addition est le ou exclusif. Cette matrice est la concaténation d'une matrice identité et d'un code. En fait les lignes de la matrice forment une base qui génère des entiers dont la distance entre-eux ne peut être inférieur à la distance entre deux lignes de la matrice (qui est aussi la distance à 0).
La distance minimum entre deux lignes de la matrice est 2 et la distance à 0 aussi. Détection d'une erreur pour transmettre 4 bits :
10001 01001 xyzt = xyzt(x^y^z^t) 00101 00011
Correction d'une erreur (non détection de 2). La distance minimum entre deux lignes de la matrice est 3 et la distance à 0 aussi. Détection d'une erreur pour transmettre 4 bits :
1000011 xyzt = xyzt(x^z^t)(x^y^z)(y^z^t) 0100101 0010110 0001111
En fait la partie droite de la matrice est dans ce cas l'énumération des entiers contenant au moins 2 bits à 1. Pour \(k\) bits de correction, on peut corriger \(2^k-k-1\) bits.
Correction d'une erreur et détection de 2 :
10001110 01001101 00101011 xyzt = xyzt(x^y^z)(x^y^t)(x^z^t)(y^z^t) 00010111
Comment on vérifie tout ça dans le cas de la correction d'un bit ? Tout simplement en recalculant le code à l'arrivée et en faisant le ou-exclusif avec le code reçu, si l'on trouve :
- 0 : tout est OK (sauf si vraiment trop d'erreur)
- Un code valide dans la matrice : Le bit faux est celui de la ligne correspondant au code valide.
- Un code avec un seul bit à 1 : La donnée est correcte, l'erreur de transmission est dans le code.
- Autre chose : il y a détection d'erreur mais pas de correction.
Turbo Code
L'idée est simple : on enchevêtre des calculs de parité afin qu'ils puissent se corriger mutuellement.
Dans l'exemple suivant, on transmet 64 bits sous la forme d'un cube 4*4*4 en ajoutant 61 bits de parité.
Le bits de parité p sont calculés suivant les 3 directions du cube.
ppppp ....p ....p ....p ....p ppppp ..@.p .@..p ....p ....p pp3p4 .@..p ..@.p ....p ..*.1 ppppp ....p ....p ....p ....p pp5p6 ppppp ppppp ppppp pp2p7
Si le bit '*' est mal transmis, 3 bits de parité seront faux. Les 3 bits faux permettent de retrouver la position du bit faux.
Si les 4 bits '@' sont mals transmis, on détecte l'erreur mais on ne peut pas la corriger car les '@' sont très mals placés, dans d'autres configurations jusqu'à 8 erreurs sont corrigeables.
Dans cet exemple, si jamais '*' est bien transmis, et 1, 2 et 3 sont mals transmis, alors 4, 5, 6, 7 et '*' indiqueront que le problème vient des bits de parité et non de la valeur transmise.
Pour qu'une séries d'erreur ne soient pas détectées, il faut qu'il y en ai au minimum 8 bien placées.
Lors du décodage, s'il y a beaucoup d'erreur, certaines ne sont pas corrigeables immédiatement. On commence donc par corriger les erreurs triviales, puis de correction en correction, des erreurs non corrigeables initialement le deviennent. Dans l'exemple précédent, si 3 des '@' sont mal transmis, alors seul l'un des 3 est initialement corrigeable.
Cette méthode est mathématiquement complexe car la façon optimale d'enchevêtrer les calculs de parité n'est pas aussi simple.
Codage de sons
Un son est produit par une variation de pression de l'air. Pour coder un son, il suffit d'échantillonner dans le temps la valeur de la pression de l'air. Les principaux paramètres stocké dans l'entête sont :
- La fréquence d'échantillonnage (8000Hz par défaut pour la voix).
- Le nombre de bits par échantillon (8 par défaut).
- Le stockage des entiers : signé ou non.
- Le nombre de canals : 1 pour mono, 2 pour stéréo
Codage d'images
On a besoin de faire un échantillonnage spatial de l'image. Pour les pixels, on a deux principaux types de codage :
- Vrai couleur : La valeur des différents canaux.
- Palette de couleur : l'indice de la couleur dans la palette.
Il faut un fichier d'entête pour tout définir.
- 1 bit: image noir et blanc
- \(n\) bits avec généralement \(1\leq n \leq 8\) : c'est un index couleur.
- \(x\) bits pour le rouge, \(y\) bits pour le vert, \(z\) bits pour le bleu : c'est une vrai couleur. C'est le modèle RVB. Il peut être réduit à 3R+3V+2B pour tenir dans un octet.
- HLS/HUV: ou autre séparant la luminance du reste pour rendre meilleur la compression.
- Des tas d'autre choix possibles
A cela il faut ajouter la correction du gamma (contraste) en effet cette connaissance est obligatoire pour que les images apparaissent de la même façon sur des écrans différents.
L'équilibrage de probabilités
La théorie de l'information définie la quantité d'information d'un événement par : \(-log_2 p(e)\) on a donc pour un ensemble d'événements indépendants E, une quantité d'information (moyenne pondérée) :
\(- \sum_{e\in E} p(e) \log_2 p(e)\)
Avec évidemment \(\sum_{e\in E} p(e)\ \ =\ \ 1\)
Application:
S'il y a 2 événements équiprobables possible : \(- 0.5 \log_2 0.5 \ - \ 0.5 \log_2 0.5 \ \ = \ \ 1\)
S'il y a 3 événements équiprobables possible : \(- 3 \frac{1}{3} \log_2 \frac{1}{3} \ \ = \ \ 1.584\)
S'il y a 2 événements avec une proba de 0.1 et 0.9 : \(- ( 0.1 \ \log_2\ 0.1 \ + \ 0.9 \log_2 0.9 ) \ \ = \ \ 0.469\)
Un fichier comportant 9 fois plus de bits à 1 que de bits à zero ne contient en fait que moitié moins d'information.
Le bug: (00 11 00 11 00 00 11 00 11 11 ...) hors contexte, 0 et 1 sont équiprobables. On se trompe donc sur la quantité d'information.... En fait, il faut regarder les événements 00 et 11... Ceci peut être étendu à l'octet dans la plupart des fichiers car on travaille rarement au niveau des chaînes de bits.
Un algorithme de compression ne peut pas compresser tous les fichiers existant, même d'un bit : Compter donc le nombre de fichiers avant et après, comme il y en a moins après, la bijection n'est pas possible.
Il est intéressant de compresser sans connaître la suite du fichier et inversement, ceci permet des algorithmes plus efficaces pour les gros fichier. Ou pour une décompression interactive : fichier Son.
Par la suite, on utilise abusivement le mot caractères, pour parler en fait d'événement.
Code de Shannon-Fano
L'idée : représenter chacun des caractères par une chaîne de bits dont la longueur est proportionnelle à la quantité d'information transporté. Les caractères rarissimes sont donc codés en utilisant plus de bits.
Comment trouver ces représentations ?
Faire la table du nombre d'occurrences.
Trier la table par nombre d'occurrences.
- Couper la table en 2 de telle manière qu'il y ai autant d'occurrences au dessus et au dessous. Entre les 2 points de coupe, choisir le meilleur.
- On ajoute à la représentation des symboles du haut le bit 0 et ceux du bas, le bit 1.
- On recommence sur chacune des 2 tables.
| A | 15 | 22 | 15 | 00 | |
| B | 7 | 7 | 01 | ||
| C | 6 | 17 | 6 | 10 | |
| D | 6 | 11 | 6 | 110 | |
| E | 5 | 5 | 111 | ||
Par construction les codes ne sont pas redondant, on n'a pas besoin de dire leur longueur. Le code donne le chemin dans un arbre binaire.
Le taux de compression ne peut dépasser 8 si cette technique est appliquée aux octets.
Il est nécessaire de passer l'arbre avant de commencer. L'arbre précédent peut être codé comme : 110A0B10C10D0E soit 49 bits pour l'arbre.
Pour la donnée elle-même : 2*(15+7+6) + 3*(6+5) → 89 bits
Un des événement doit être le celui indiquant la fin de fichier (obligatoire car le système ne donne la taille des fichiers qu'en octet...)
Décodage simple
L'algo stupide est un boucle infini contenant :
SI état courant = feuille de l'arbre
ALORS
Prendre en compte l'événement considéré
Retourner à la racine
SINON
Lire le bit suivant
SI bit 0
ALORS état courant passe dans la branche de gauche
SINON état courant passe dans la branche de droite
Cette algorithme est excessivement lent car les processeurs ne sont pas fait pour traiter des bits un par un.
Décodage rapide
L'algo intelligent fait une lecture paquet de bits par paquet de bits en parcourant l'arbre plusieurs étapes à la fois. Là aussi une boucle infini.
typedef struct { unsigned int bits:9 ; /* Bits restant à lire */ unsigned int feuille:1 ;/* Vrai si feuille */ unsigned int numero:8 ; /* Numéro feuille ou noeud */ } Etat ; Etat table[255][512] ; /* [numero_noeud][bit_a_lire] */ void decode() { Etat courant ; int c ; courant.feuille = 0 ; courant.numero = 0 ; courant.bits = 1 ; for(;;) { if ( courant.feuille ) { /* Faire l'action (qui peut être EOF) */ printf("%d", courant.numero ) ; /* '[0]' car on repart de la racine */ courant = table[0][courant.bits] ; } else { /* Plus de bits dans 'bits' */ c = getchar() ; if ( c<0 ) exit(1) ; // Ceci ne doit JAMAIS arriver courant.bits = 256 + c ; courant = table[courant.numero][courant.bits] ; } } }
Remarque : Une chaine de bits à traiter est préfixée par un bit à 1.
Code de Huffman
Les codes Huffman sont toujours légèrement meilleurs que les codes de Shannon-Fano.
On relie ensemble les symboles ou groupes de symboles de plus faible probabilité jusqu'à obtenir une table avec un seul élément.
| 0 | A | 15 | 39 | |||
| 100 | B | 7 | 13 | 24 | ||
| 101 | C | 6 | ||||
| 110 | D | 6 | 11 | |||
| 111 | E | 5 | ||||
Pour la donnée elle-même : 1*15 + 3*(7+6+6+5) → 87 bits
Le décodeur est identique au décodeur vu pour Shannon-Fano.
Événements dépendents.
Si un événement dépend de l'événement précédent, alors on va calculer la probabilité de l'événement en fonction de l'événement précédent. Il y aura donc autant de manière de coder qu'il y a d'événements. Dans un texte français la probabilité du 'u' après un 'q' est de 95%, lettre 'u' sera donc codée sur un seul bit si elle est après un 'q'.
La taille des tables est exponentielle en fonction du nombre d'événement précédents que l'on prend en compte. Il n'est donc pas possible transférer tous les arbres du compresseur au décompresseur.
Le codage adaptatif
Il est permet de ne pas transférer les arbres. Le compresseur et le décompresseur sont initialisés avec le même arbre (ou les mêmes arbre) contenant un seul symbole : Escape. L'algorithme est le suivant :
| Coté compresseur | Coté décompresseur |
|---|---|
| Lecture d'un événement | Lecture d'un code |
| Cet événement est dans l'arbre : on envoit son code | Ce n'est pas Escape : on a bien décodé l'événement |
| Cet événement n'est dans l'arbre : on envoit le code de Escape suivi de l'événément tel quel. | C'est Escape : on lit un événement tel quel. |
| On met à jour l'arbre car les probabilités ont changé ou un nouvel événement à été ajouté à l'arbre | |
La difficulté est évidemment la mise à jour de l'arbre qui doit être rapide. On peut s'en sortir en faisant un arbre de poid trié. Et à chaque incrément, mettre à jour l'arbre si le tri n'est pas respecté. On peut aussi mettre à jour l'arbre seulement tous les X événements.
Limitations de l'approche
Les taux de compressions ne peuvent pas être extraordinaires car un événement est codé au mieux sur un seul bit. C'est dommage car quand on tient compte des événements précédents, certaines probabilités sont égales à 1 . Par exemple le 's' final de ' êtes' en français.
Dans le cas de fichier non uniformes, par exemple français au début et anglais à la fin, l'équilibrage des probabilités ne se fera pas bien. L'astuce est d'utiliser des codes save et restore qui permette d'enregistrer et restaurer les arbres. Le changement d'arbre est une décision complexe qui est à la charge du compresseur. Le décompresseur se contente de suivre les instructions.
Codage arithmétique (range encoder)
C'est l'équilibreur de probabilité optimal, les événements sont codés par un nombre de bits égal aux nombre de bit d'informations transportés. On peut donc coder des événements sur moins d'un bit.
L'idée : on code le fichier complet par un nombre flottant entre 0 et 1 qui possède une précision suffisante.
Exemple : on veut coder tet :
Codage :
Décodage :
|
Les algorithmes de compression et décompression peuvent directement être programmé en C dans des double si le nombre de bits à stocker n'est pas trop important. Ceci n'empêche pas de stocker des milliers d'événements dans un seul double.
Soit \(p(i)\) la probabilité de l'événement numéro \(i\).
Soit \(S(i) = \sum_{j<i} p(j)\)
| Algo de compression | Algo de décompression |
|---|---|
double somme = 0 ;
double taille = 1 ;
Pour les événements i :
{
somme += S(i) * taille;
taille *= p(i) ;
}
|
Tant que pas de fin fichier
{
Soit i Tq S(i) < somme < S(i+1)
Faire l'action i
somme -= S(i) ;
somme /= p(i) ; // entre 0 et 1
}
|
Le précision (indépendante de l'ordre des caractères) sera la largeur de l'intervalle : \(\prod_{e \in E} p(e)^{\text{nbcar}}\)
Exemple numérique : 1000000 de caractères dont 10 'A' et 999990 'B' \(\left( \frac{1}{100000}\right) ^{10} * \left( \frac{99999}{100000}\right) ^{999990} = 4.54 10^{-55}\)
Soit 181 bits pour coder ce nombre.
Dans la réalité on ne calcule pas avec tous les chiffres significatif, on bidouille en utilisant des notations flottantes redondantes.
C'est une méthode lente.
Asymmetric Numeral Systems (ANS)
Compresse autant que le codage arithmétique mais 30 fois plus rapide. Il peut même être plus rapide que Huffman pour le décodage statique. Découverte par Jarosław (Jarek) Duda (2007), maintenant utilisé dans différentes variantes par toutes les nouvelles méthodes de compression.
Contrairement aux autres méthodes, la décompression extrait les symboles dans l'ordre inverse de leur compression.
La suite de symboles est codée par un entier, le message vide est l'entier 1. La table suivante contient la liste des premiers messages dans le cas de 2 symboles A de probabilité ¼ et B de probabilité ¾.
| Entier | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| Symbole | A | B | B | B | A | B | B | B | A | B | B | B | A | B | B | B | A |
| Numéro | 0 | 0 | 1 | 2 | 1 | 3 | 4 | 5 | 2 | 6 | 7 | 8 | 3 | 9 | 10 | 11 | 4 |
| Message | B | BB | A | BBB | AB | BBBB | BA | ABB | BBBBB | BAB | BBA | ABBB | BBBBBB | BABB | AA |
Encodage d'un symbole :
entier := e Tel que Symbole[e] == symbole et Numéro[e] == entier
Décodage d'un symbole :
symbole := Symbole[entier] entier := Numéro[entier]
On peut implémenter cette méthode sans utiliser de tableaux et en faisant des calculs sur des entiers longs. Mais dans ce cas elle est aussi longue que le codage arithmétique.
On peut par contre, moyennant une perte de compression la transformer en une méthode extrêmement rapide et permettant la transmission progressive (tANS). Au lieu de travailler sur des entiers de longueur quelconque on boucle quand on déborde. Pour le décodage, les entiers peuvent éventuellement avoir plusieurs prédécesseurs, pour choisir le bon on doit donc lire un certain nombre de bits dépendant du nombre de prédécesseurs possibles.
Avec l'exemple précédent, on peut prendre les entiers de 0 à 7 et obtenir par exemple :
| Entier | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Symbole | A | B | B | B | A | B | B | B |
| Suivant | A→0 B→1 | A→4 B→2 | A→0 B→3 | A→4 B→5 | A→0 B→6 | A→4 B→7 | A→0 B→1 | A→4 B→2 |
| Précédent | 0 1 4 6 | 0 6 | 1 7 | 2 | 1 3 5 7 | 3 | 4 | 5 |
| Nb bits | 2 | 1 | 1 | 0 | 2 | 0 | 0 | 0 |
Le décodeur :
- Lit l'entier final
- Génère le symbole
- Lit le nombre de bits indiqué par l'entier pour trouver l'entier précédent. Cela peut être 0
Remarques :
Le tableau définissant le graphe de changement d'état va influencer sur le taux de compression, il existe différente manières pour le trouver.
Cette méthode fonctionne quelque soit le nombre de symboles.
- Cette méthode n'est pas adaptée pour du codage adaptatif car le calcul
de la table de changement d'état est trop coûteux.
- Il suffit de mélanger les symboles initiaux pour crypter le message sans coût CPU supplémentaire.
- Pour mieux comprendre : affichage graphique d'ANS
Compression de données
La compression de données doit ce faire sans perte quelque soit les données à comprimer.
Les méthodes sont présentées dans leur ordre de découverte.
LZ77
Créé par Abraham Lempel et Jacob Ziv en 1977.
C'est la méthode qui permet d'obtenir la décompression la plus rapide qu'il soit possible de faire. En effet, le décompresseur reçoit des triplets :
- Une position relative dans le texte déjà décomprimé par rapport à l'endroit où l'on est.
- La longueur du texte à la position indiqué qu'il faut recopier à l'endroit où l'on est. Cette longueur peut être nulle.
- Un caractère à ajouter tel quel au fichier.
Le compresseur doit trouver dans le texte déjà envoyé la chaine la plus longue correspondant à ce qui reste à comprimer.
| D | A | DADA | .DADD | Y | .DADO | OOOA | Pos | Len | Char | |
|---|---|---|---|---|---|---|---|---|---|---|
| D | 0 | 0 | D | |||||||
| A | 0 | 0 | A | |||||||
| 1 | 1 | . | ||||||||
| DADA | 3 | 3 | A | |||||||
| .DADD | 4 | 4 | D | |||||||
| Y | 0 | 0 | Y | |||||||
| .DADO | 5 | 4 | O | |||||||
| OOOA | 0 | 3 | A |
Les valeurs des triplets sont encodés en passant dans 3 équilibreurs de probabilités différents car les probabilités ne sont pas les mêmes.
La taille du buffer est a ajusté en fonction de la donnée à comprimer et du temps de calcul que l'on souhaite utiliser. Prendre un petit buffer permet de faire une compression locale.
LZ78
On remplace le couple position/longueur par un numéro de chaine. Lors de chaque envoi de chaine, une nouvelle chaine est créée, contenant la chaine envoyée + le caractère envoyé.
| D | A | DA | DA. | DAD | DY | . | DADO | O | OO | A | Str | Char | New | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0: | ||||||||||||||
| D | 0 | D | 1: D | |||||||||||
| A | 0 | A | 2: A | |||||||||||
| 1 | . | 3: D. | ||||||||||||
| DA | 1 | A | 4: DA | |||||||||||
| DA. | 4 | . | 5: DA. | |||||||||||
| DAD | 4 | D | 6: DAD | |||||||||||
| DY | 1 | Y | 7: DY | |||||||||||
| . | 0 | . | 8: . | |||||||||||
| DADO | 6 | O | 9: DADO | |||||||||||
| O | 0 | O | 10: O | |||||||||||
| OO | 10 | O | 11: OO | |||||||||||
| A | 2 | ? | ? |
La localité disparait pour les gros fichiers. Il faut donc avoir des actions permettant de manipuler les dictionnaires.
LZW
Implémentation de Terry Welch en 1984.
On préencode les 256 caractères dans 256 chaines.
La chaine créée est la précédente envoyée + le premier caractère de celle que l'on vient d'envoyer.
| D | A | D | . | DA | DA | .D | AD | D | Y | .DA | D | O | O | OO | A | Char | New |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D | D | ||||||||||||||||
| A | A | 256: DA | |||||||||||||||
| D | D | 257: AD | |||||||||||||||
| . | . | 258: D. | |||||||||||||||
| DA | 256 | 259: .D | |||||||||||||||
| DA | 256 | 260: DAD | |||||||||||||||
| .D | 259 | 261: DA. | |||||||||||||||
| AD | 257 | 262: .DA | |||||||||||||||
| D | D | 263: ADD | |||||||||||||||
| Y | Y | 264: DY | |||||||||||||||
| .DA | 262 | 265: Y. | |||||||||||||||
| D | D | 266: .DAD | |||||||||||||||
| O | O | 267: DO | |||||||||||||||
| O | O | 268: OO | |||||||||||||||
| OO | 268 | 269: OOO | |||||||||||||||
| A | ? | ? |
C'est une méthode brevetée, mais qui est maintenant dans le domaine publique. Elle était notamment utilisée compresser les images GIF dans le premier compresseur de fichier Unix (extension .Z).
Cet algorithme n'a besoin que d'un seul égaliseur de probabilités. On peut remarquer que plus les codes sont anciens, moins ils sont utilisés. Il est donc plus intéressant pour augmenter la redondance de coder les numéros de chaine comme le nombre de chaines moins le numéro d'ordre. Les chaines récentes qui ont le plus de chance d'être utilisées, sont donc codées par de petits entiers.
Blocksorting (bzip)
Cet algorithme comprime par bloc de donnée de plusieurs centaines de kilo octets.
Voici le principe exemplifié avec le bloc 'BANANE' :
On peut suprimer les répétitions dans le bloc initial en faisant du RLE (Run Length Encoding). En code le nombre de répétitions et le caractère à répéter.
On crée une matrice carré virtuelle contenant les textes décalés.
BANANE (*) Chaine initiale ANANEB NANEBA ANEBAN NEBANA EBANANOn trie les lignes.
ANANEB ANEBAN BANANE (*) Chaine initiale EBANAN NANEBA NEBANAOn extrait la dernière colonne qui dans les cas réels contient de nombreux caractères identiques successifs : BNENAA
On applique l'algorithme MTF (Move To Front) qui maintient un tableau dont les éléments les plus courants ont le indices les plus petits. Le dernier élément envoyé prend toujours l'indice 0.
B:66 N:78 E:70 N:1 A:65 A:0 On peut appliquer des prétraitements (RLE) de supression des répétitions de 0 qui seront les plus courantes.
Sur un exemple réel, les codes comportent de très nombreux entiers avec une faible valeur numérique. Le codage arithmétique donne le meilleur résultat, mais on peut se contenter de Huffman.
Pour décompresser.
On obtient directement la première colonne en triant les lettres de la dernière.
On parcour chacune des lignes du tableau de la première à la dernière. Pour chaque ligne on lui associe comme successeur la première ligne qui commence par le dernier caractère de la ligne courante et qui n'a pas encore de prédécesseur.
Ceci fonctionne uniquement parce que la liste est triée et donc l'ordre des lettres identiques à droite est le même que l'ordre des lettres identiques à gauche !
1 ANANEB 3 2 ANEBAN 5 3 BANANE 4 4 EBANAN 6 le 5 est déjà pris 5 NANEBA 1 6 NEBANA 2On parcourt à partir de la ligne contenant le bon décalage, la liste circulaire créée dans le sens inverse : 3, 1, 5, 2, 6, 4
On obtient donc en gardant les premières lettres : B A N A N E
Le compresseur permet de comprimer efficacement de gros blocs même s'ils sont hétérogènes car le tri permet de remettre ensemble les chaines similaires.
LZMA2
C'est actuellement le meilleur algorithme de compression généraliste. Il y a de nombreuses implémentations différentes de l'idée de base. C'est lui qui est utilisé dans 7zip.
Cet algorithme est en fait LZ77, la seule différence siginification est que l'on ne génère pas des triplets mais des paquets de différents types.
| Paquet | Commentaire |
|---|---|
| 0 + octet | Envoit un octet. |
| 10 + len + dist | Distance et position de la chaine à recopier. |
| 1100 | Distance: dernière utilisée, longueur: 1 |
| 1101 + len | Distance: dernière utilisée |
| 1110 + len | Distance: avant dernière utilisée |
| 11110 + len | Distance: avant avant dernière utilisée |
| 11111 + len | Distance: avant avant avant dernière utilisée |
Les longueurs sont généralement courtes. Le codage optimise donc le transfert des petites valeurs.
| Longueur | Interval |
|---|---|
| 0 + 3 bits | 2-9 |
| 10 + 3 bits | 10-17 |
| 11 + 8 bits | 18-273 |
Les distances sont codées par un numéro de slot sur 6 bits suivi d'un certain nombre de bits dépendant du slot. Certains bits du codage sont fixes car équiprobable, d'autres passent par le codeur arithmétiques.
Toutes les valeurs codées passent par un codeur arithmétique dont les tables dépendent des types des derniers paquets envoyés et du type de la valeur à coder. Tout ceci donne plus de 1000 tables contenant des probabilités.
Compression d'images binaires sans pertes
La compression d'image ou les pixels sont codés dans des octets se fait assez bien avec les algorithmes de compression de données. Par contre les résultats pour les images binaires (bitmap) sont décevants.
RLE et FAX
Le codage RLE (Run Length Encoding) est ancien et simple pour coder les images. Il est surtout utilisé pour des images non-naturelles (sans bruit). Chaque pixel est précédé du nombre de répétitions de ce pixel.
Les FAX (FAC Simile) utilisent ce principe en l'améliorant au maximum. (Groupe 1: analogique, 2: numérique, 3: compression 1D (2D option), 4 compression 2D). Les FAX devait à l'époque fonctionner avec des capacités mémoire et CPU très faible.
Les tables de probabilités ont été statiquement optimisées en fonctions des types de document que l'on souhaitait transmettre par FAX.
Quand on décode, il y a une couleur courante (noir ou blanc) et un mode définissant l'ensemble des instructions possibles.
Mode normal :
| Bits lus | Action |
|---|---|
| 001 Len Len | Affiche une bande de la couleur courante et une de la couleur opposée à la couleur courante. Le codage des longueurs dépend de la couleur. |
| 0001 | Affiche une bande de couleur de la même longueur qu'une alternance de couleur sur la ligne du dessus. |
1
011
010
000010
000011
0000010
0000011
|
Vertical(0)
Vertical(-1)
Vertical(1)
Vertical(2)
Vertical(-2)
Vertical(3)
Vertical(-3)
On écrit avec la couleur courante une bande de la même longueur que la bande au dessus avec un décalage à la fin. La couleur courante bascule. |
| 0000001xxx | Réservé pour de futures extensions. |
| 0000001111 | Passage en mode non compressé. |
Codage des longueurs : elles ne sont pas toutes codables pour éviter d'avoir des tables trop grosses.
| Longueur | Blanche | Noire |
|---|---|---|
| 0 | 00110101 | 0000110111 |
| 1 | 000111 | 010 |
| 2 | 0111 | 11 |
| 3 | 1000 | 10 |
| 4 | 1011 | 011 |
| 5 | 1100 | 0011 |
| 6 | 1110 | 0010 |
| 7 | 1111 | 00011 |
| 8 | 10011 | 000101 |
| 9 | 10100 | 000100 |
| ... | ... | ... |
| 63 | 00110100 | 000001100111 |
| 64 | 11011 | 0000001111 |
| 128 | 10010 | 000011001000 |
| 192 | 010111 | 000011001001 |
| ... | ... | ... |
| 1728 | 010011011 | 0000001100101 |
Mode non compressé :
On revient au mode normal en émettant un code se terminant par T. La couleur courant prend comme valeur T. Ce codage perd pas de la place seulement s'il y a plus de 5 pixels '0' (noir) de suite.
| Pixels | Code |
| 1 | 1 |
| 01 | 01 |
| 001 | 001 |
| 0001 | 0001 |
| 00001 | 00001 |
| 00000 | 000001 |
| 0000001T | |
| 0 | 00000001T |
| 00 | 000000001T |
| 000 | 0000000001T |
| 0000 | 00000000001T |
JBIG
On suppose les pixels codés sur un bit.
On suppose que la compression est faite pixel par pixel dans le sens de la lecture. Ceci implique que le décompresseur connaît tous les pixels au dessus et les pixels sur la même ligne, à gauche du pixel courant.
Pour évaluer la probabilité de X, on va prendre en compte 10 pixels (par exemple) parmis les précédents pour évaluer la probabilité que le pixel courant soit blanc ou noir. Il y a donc 1024 tables de probabilité contenant 2 événements possibles. Les pixel '?' sont inconnus car non encore transférés. Les cases vides sont des pixels connus dont on ne tient pas compte pour ne pas multiplifier le nombre de tables inutilement.
| 0 | 1 | 2 | ||
| 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | X | ? | ? |
On peut coder l'image en multi-résolution. Une image à faible résolution est d'abord envoyée avec la méthode précédente. Pour les autres images, on va tenir compte de 6 pixels précédents de l'image courante et de 4 pixels de l'image à résolution inférieure qui est deux fois plus petite. Ceci permet de tenir compte de la suite de l'image pour comprimer le pixel courant, dans certain cas, la probabilité peut atteindre 1. Il y a 4 cas différents suivant la parité des coordonnées du pixel.
Le codage des images en niveau de gris peut être fait bitmap par bitmap en utilisant les codes de Gray pour minimiser le bruit.
JBIG comprime deux fois plus que l'algo présenté pour les FAX. Il est très souvent employé dans les FAX (normé en 1993). Depuis 2012 il n'y a plus de brevets empêchant son utilisation.
Compression de signal
La compression de signal a certaines particularités :
- Des régularités, répétitions.
- Des continuités de valeur ou de variation de valeur.
- Du bruit : mauvaise compression classique.
- La précision absolue n'est pas nécessaire.
Les idées pour la compression :
- Codage relatif, on compresse la dérivée.
- Codage prédictif, on compresse la différence par rapport à la dérivée.
- Élimination des haute fréquences (non visibles, inutiles, capteur).
Dans tous les cas, la méthode se termine par un équilibrage de probabilité pour coder les informations de manière efficace.
Réduire la précision du signal ou le transformer
Dans le cas des images, il est possible de réduire le nombre de couleurs utilisées en passant par une étape de quantification.
Une fois la palette de couleur définie, on peut soit :
- remplacer la couleur de chaque pixel par la couleur la plus proche de la palette. Dans ce cas on verra de grandes zones de couleur uniforme si la palette contient trop peu de couleur.
- remplacer globalement les couleurs sur un ensemble de pixel pour simuler un dégradé. C'est ce qui est utilisé pour l'impression papier, ce sont les très nombreuses techniques de dithering
Pour passer de couleur en niveau de gris :
Luminance = 0.3 Rouge + 0.59 Vert + 0.11 Bleu
Dans tous les cas, si quelques valeurs dans le signal empêchent d'obtenir un bon taux de compression, il faut les raboter car ces valeurs étant rares elles ne seront pas visibles pour un être humain.
Prédiction
Un signal est une fonction généralement continue et régulièrement échantillonnée.
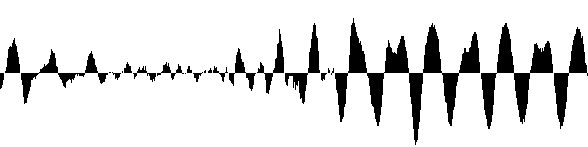
On stocke la différence entre la valeur réelle du signal et la prédiction que l'on en a faite. Cette valeur est normalement très petite si la prédiction est correcte.
On peut donc faire la déduction suivante pour un signal 1D continu :
\(V_{i+1}\ \approx\ V_{i}\)
On voit que les valeurs nécessaires pour coder le signal sont bien plus petites :
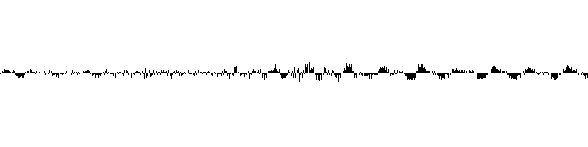
La dérivé est généralement continue :
\(V_{i+1} - V_{i}\ \approx\ V_{i} - V_{i-1}\)
\(V_{i+1}\ \approx\ 2V_{i} - V_{i-1}\)
On voit que les valeurs nécessaires pour coder le signal sont encore plus petites que dans le cas précédent :
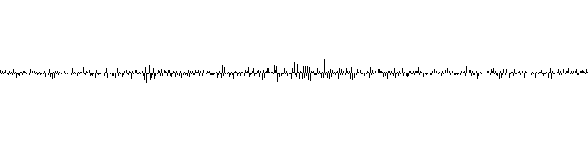
Si l'on va jusqu'à la dérivée seconde :
\(( V_{i+1} - V_{i} ) - ( V_{i} - V_{i-1} )\ \approx\ ( V_{i} - V_{i-1} ) - ( V_{i-1} - V_{i-2} )\)
\(( V_{i+1} - V_{i} ) \ \approx\ 2( V_{i} - V_{i-1} ) - ( V_{i-1} - V_{i-2} )\)
\(V_{i+1}\ \approx\ V_{i} + 2( V_{i} - V_{i-1} ) - ( V_{i-1} - V_{i-2} )\)
\(V_{i+1}\ \approx\ 3V_{i} - 3V_{i-1} + V_{i-2}\)
Le son donné en exemple est très bruité, il suffit d'écouter le fichier audio pour s'en rendre compte. Pour ce signal, passer à la dérivée seconde fait diminuer le taux de compression et n'est donc pas intéressant. La dynamique des valeurs suivantes est plus grande.
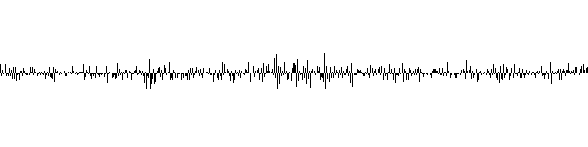
MP3
Les algorithmes de prédiction ne sont pas suffisant pour compresser le son. Pour pouvoir compresser fortement du son, il faut se rapprocher de sa nature, ce sont des oscillations qui s'ajoutent les unes aux autres. Il faut donc travailler dans le domaine fréquentiel.
Si l'on veut transmettre un son stéréo, on transmet la moyenne des deux sons ainsi que la différence. Cela augmente le taux de compression et permet de facilement oublier la stéréo en gardant le mono sans perte de qualité.
DCT : Transformée cosinus discrète
C'est la transformation généralement utilisée dans tous les compresseurs de son avec des variations. Elle travaille bloc par bloc, l'utilisation de grand bloc permet d'augmenter le taux de compression mais introduit un latence inacceptable pour une utilisation interactive (téléphone).
Le son à compresser est dans un tableau de flottant \(s\) dont les indices commencent à 0 et contenant \(n\) échantillons.
\(s'\) est le résultat de l'application de la DCT à \(s\) :
\(s'[i] = \frac{\sqrt{2}}{\sqrt{n}} \sum_j \frac{s[j]}{i=0 ? \sqrt{2}:1} \cos\left( i \pi \frac{ 2j+1 }{2n} \right)\)
\(s'[0]\) est la valeur moyenne du signal qui est généralement nulle pour un son. Ceci correspond à une fréquence nulle.
- Si le bloc dure une seconde :
- \(s'[i]\) est l'énergie transportées par la fréquence \(i/2\)
- donc \(s'[1]\) est donc la fréquence ½Hz
- Si bloc contient 8000 échantillons, \(s'[7999]\) est l'amplitude de la fréquence \(\frac{7999}{2}\) Hz. Le théorème de Shannon indique que l'on doit obligatoire échantillonner au double de la fréquence maximum pour ne pas perdre d'information.
On voit alors dans \(s'\) que l'information se résume à quelques pics, le reste étant pratiquement nul. L'image suivante représente 8 blocs mis les uns après les autres. En effet au lieu de travailler sur un son complet, on travaille sur une partie du son car l'algorithme précédent est en temps \(O(n^2)\)
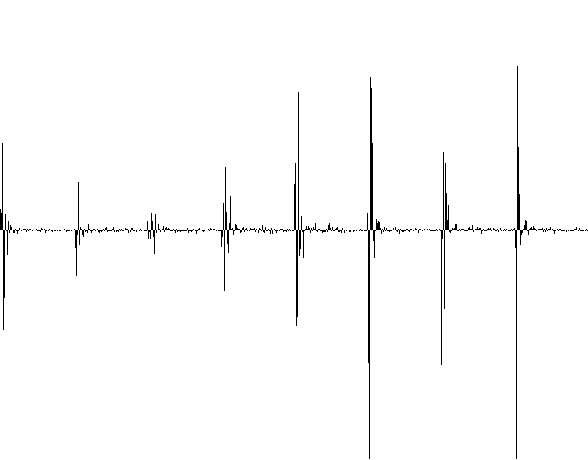
La transformée inverse est égale à :
\(s[i] = \frac{\sqrt{2}}{\sqrt{n}} \sum_{j} \frac{s'[j]}{j=0 ? \sqrt{2}:1} \cos \left( j \pi \frac{ 2i+1 }{2n} \right)\)
Comme vous le voyez, c'est exactement la même formule appliquée en inversant les indices. On peut donc exprimer le calcul comme un produit matrice/vecteur (voir la partie sur le JPEG).
On peut faire les calculs en virgule fixe (et donc en entier). Mais dans ce cas, on ne retrouve pas exactement le signal de départ lorsque l'on applique la formule inverse.
Générateur de table de sinus
Pour tracer un cercle, on part du point \(\left( \begin{matrix} 1 \\ 0 \end{matrix} \right)\) et on lui applique une suite de rotation d'angle \(\epsilon\) on obtient alors la suite des sinus et cosinus.
La matrice de rotation avec son déterminant égal à 1 est :
\(\left( \begin{matrix} cos(\epsilon) & -sin(\epsilon) \\ sin(\epsilon) & cos(\epsilon) \end{matrix} \right)\)
Epsilon étant petit, on peut prendre les approximations suivantes en négligeant \(\epsilon^2\), on a alors : \(cos(\epsilon) = 1\) et \(sin(\epsilon) = \epsilon\)
La matrice est alors : \(\left( \begin{matrix} 1 & -\epsilon \\ \epsilon & 1 \end{matrix} \right)\) mais son déterminant étant de \(1 + \epsilon^2\) ce n'est pas une matrice de rotation.
Heureusement, un informaticien incompétent passe par là et code ce produit matrice vecteur de cette façon avec les calculs faits en virgule fixe :
int virgule_fixe = 1<<24 ; // 24 bits après la virgule int inverse_epsilon = 1<<16 ; // epsilon = 1/(1<<16) int x = virgule_fixe ; // Valeur réelle : 1 int y = 0 ; while(x > y) // Un quart cercle { x -= y / inverse_epsilon ; y += x / inverse_epsilon ; }
Ce programme est faux car 'y' utilise la nouvelle valeur de 'x' au lieu de l'ancienne. Il calcule en fait le produit avec la matrice :
\(\left( \begin{matrix} 1 & -\epsilon \\ \epsilon & 1 - \epsilon^2 \end{matrix} \right)\)
Et par miracle cette matrice a un déterminant égal à 1, c'est donc une matrice de rotation.
Cette algorithme est souvent utilisé car lorsqu'il est optimisé le temps de calcul est plus rapide que l'accès à un tableau précalculé en mémoire. Ceci évidemment avec les processeurs actuels.
Psycho acoustique
Des tests ont montrés que l'oreille humaine ne peut discerner des fréquences proches et de puissances différentes. Une fréquence de forte amplitude cache les fréquences proches et moins fortes.
Ce phénomène se produit aussi dans le temps, un son peut être masqué par un son qui s'est produit 50ms avant ou se produira 100ms après.
Il n'y a pas de formule mathématique associée à ces résultats, mais des tables de valeurs expérimentales indiquant les endroits où la perte d'information est inaudible. Ces tables font parties de normes qui sont payantes. Après la perte d'information, le son n'est donc plus du tout le même mais c'est indiscernable à l'oreille humaine.
Méthode stupide pour gagner de la place
Si les calculs sont fait en 8 bits signé, si l'on a un pique en \(i\) de hauteur \(h\), on peut annuler l'amplitude des fréquences qui sont à une distance \(d\) du pique et de puissance inférieure à \(h - \frac{256(d-i)}{n}\).
Les puissances sont en valeur absolue. Si l'on déborde de la bande passante allouée, on peut détériorer un peu plus le son pour réduire encore la taille de son codage.
Méthode plus souple pour gagner de la place
On utilise moins de bits pour stocker l'information quand une fréquence est cachée.
Pour faire cela, on divise la valeur à coder par 2 si l'on veut perdre 1 bit, 4 si l'on veut perdre 2 bits... Au moment du décodage, il faut faire la multiplication dans l'autre sens. Ceci nécessite d'être capable de retrouver le coefficient diviseur.
Méthode astucieuse pour gagner de la place
Au moment du codage, on met à 0 un certain nombre de bits de poids faibles.
La probabilité des entiers se terminant avec des bits à 0 sera alors plus grande et ils seront donc codés sur moins de bits.
Codage
- Le codage utilisé est une répétition de paires :
- Nombre de valeurs égales à 0 dans \(s'\)
- La valeur différente de 0
- Le nombre de 0 est codé comme suit :
- Le nombre de bits du nombre à coder (indiqué par le préfixe du tableau)
- suivi de la valeur du nombre à coder moins le bit de poid fort.
| Nombres codés | Nb bits | Préfixe | Suffixe |
|---|---|---|---|
| 0 | 0 | 00 | vide |
| 1 (pas 0) | 1 | 010 | vide |
| 2-3 | 2 | 011 | 2=0 3=1 |
| 4-7 | 3 | 1000 | 4=00 5=01 6=10 7=11 |
| 8-15 | 4 | 1001 | 8=000 9=001 10=010… |
| 16-31 | 5 | 1010 | 16=0000 17=0001… |
| 32-63 | 6 | 1011 | 32=00000 33=00001… |
| 64-127 | 7 | 1100 | 64=000000 65=000001… |
| 128-255 | 8 | 1101 | 128=0000000… |
| 256-511 | 9 | 1110 | 256=00000000… |
| 512-1023 | 10 | 1111 | 512=000000000… |
Pour des nombres signés, on ajout le bit de signe, on ne met toujours pas le bit de poid fort car il est toujours égale à 1.
Vous pouvez chercher de meilleurs codages mais je doute que vous en trouviez.
N'oubliez pas qu'une des contraintes et de pouvoir décompresser sans attendre la suite.
Divers
La compression est d'un facteur 6 sans perte de qualité audible par un auditeur non entrainé à détecter les artefacts de compression.
Artefacts du au fait qu'après décompression avec perte, il y a une discontinuité du signal entre chaque bloc.
JPEG
La compression JPEG (Joint Picture Expert Group) permet de comprimer des images en tenant compte d'un facteur de qualité. Le standard ne formalise que la manière de décomprimer.
Le compression d'image couleur se fait en compressant indépendemment les 3 composantes (pas RVB mais YUV ou un autre du même genre afin de rendre indépendant les canaux). On détaillera le cas d'image en niveau de gris.
La compression d'image se fait étonnament de la même manière que celle du son. La principale différence sera la façon de dégrader le signal. Contrairement au son, le signal n'a pas une moyenne nulle et il est 2D.
La DCT 2D est une DCT dans un sens puis dans l'autre. On peut réécrire la DCT comme un produit de matrice.
\(DCT(j, i) = \frac{\sqrt{2}}{\sqrt{n}} \cos( j \pi \frac{ 2i+1 }{2n} )\)
\(DCT(0, i) = \frac{1}{\sqrt{n}}\)
En JPEG, la taille de la matrice DCT a été fixée (par les experts) à 8×8 afin que l'algorithme puisse être codé directement sur le silicium. Voici la matrice DCT 8×8 avec les basses fréquences en haut à gauche et les hautes en bas à droite :
+0.3536 +0.3536 +0.3536 +0.3536 +0.3536 +0.3536 +0.3536 +0.3536 +0.4904 +0.4157 +0.2778 +0.0975 -0.0975 -0.2778 -0.4157 -0.4904 +0.4619 +0.1913 -0.1913 -0.4619 -0.4619 -0.1913 +0.1913 +0.4619 +0.4157 -0.0975 -0.4904 -0.2778 +0.2778 +0.4904 +0.0975 -0.4157 +0.3536 -0.3536 -0.3536 +0.3536 +0.3536 -0.3536 -0.3536 +0.3536 +0.2778 -0.4904 +0.0975 +0.4157 -0.4157 -0.0975 +0.4904 -0.2778 +0.1913 -0.4619 +0.4619 -0.1913 -0.1913 +0.4619 -0.4619 +0.1913 +0.0975 -0.2778 +0.4157 -0.4904 +0.4904 -0.4157 +0.2778 -0.0975
La compression de son se réécrit comme \(s' = DCT * s\) et sa décompression comme \(s = DCT^T * s'\)
Donc en 2D, pour l'image \(I\), sachant que \((A*B)^T=B^T*A^T\) on a :
\(I' = ( DCT * ( DCT * I ) ^ T ) ^ T = DCT * I * DCT^T\)
Image initiale affichant un dégradé de gris bruité :
+45 +55 +63 +75 +85 +90 +100 +105 +60 +72 +80 +89 +90 +109 +117 +116 +77 +93 +102 +99 +116 +127 +127 +133 +98 +97 +116 +127 +135 +133 +136 +149 +105 +123 +124 +140 +143 +147 +162 +173 +125 +134 +149 +153 +154 +164 +168 +177 +142 +149 +160 +172 +168 +191 +184 +199 +153 +169 +168 +177 +198 +203 +205 +219
Le résultat \(I'\) est une matrice qui contient des nombres généralement petits. Cette étape permet déjà de comprimer l'image. La DCT de l'image précédente :
+1051.8 -147.7 -9.7 -17.3 -2.5 -7.9 +2.7 -5.7 -283.1 -1.1 -1.9 +1.7 -3.9 +4.9 -3.3 +4.6 +0.3 -8.0 +2.9 +6.9 -4.3 -2.9 -0.8 -2.6 -33.6 +1.8 +1.1 -7.0 +1.6 +7.8 -2.3 -3.6 +2.7 -6.9 -0.7 -0.1 +11.5 -4.5 -8.1 +4.6 -6.9 +5.8 -6.0 +1.2 +6.1 +2.0 +9.1 +0.3 +0.1 +2.6 -1.0 +1.2 -2.5 -7.3 -0.6 +7.4 +2.3 -6.0 +4.5 -0.4 -4.5 -5.0 -3.8 -3.5
L'inverse de la DCT :
\(I = (DCT^T * (DCT^T * I')^T) ^ T = DCT^T * I' * DCT\)
Pour la qualité, le principe n'a rien à voir avec ce qui est fait pour le son. Pour les images, on se contente dire que l'on a pas besoin des hautes fréquences et donc on les code avec moins de précision. Cette quantification est paramétrable, elle ressemble à :
\(I''(i,j) = \frac{I'(i,j)}{1+(i+j+1)Q}\)
Où \(0<Q<25\) est le facteur de qualité, 0 étant la meilleure. La DCT de l'image précédente quantifiée avec Q=1 :
+526 -48 -1 -2 0 0 0 0 -93 0 0 0 0 +1 0 0 0 -1 0 +1 0 0 0 0 -6 0 0 0 0 +1 0 0 0 0 0 0 +1 0 0 0 0 +1 0 0 +1 0 +1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Dans le bas-droite de \(I''\) il y a beaucoup de 0. On ne va donc pas coder \(I''\) ligne par ligne mais en zig-zag.
Le codage se fait ensuite comme la DCT sur les sons.
Voici la différence entre l'image compressée avec perte et l'image initiale:
-12 +6 -1 -3 +2 -1 0 +1 +1 0 +2 +3 -3 +3 -3 +2 -3 +2 +3 -4 +3 +4 0 -1 -3 -4 +1 +3 +4 0 0 -4 -2 +4 0 +3 +1 0 0 +9 0 0 +5 +3 0 -1 -9 0 -5 0 -1 +5 -8 +4 -1 +1 0 +3 +1 0 +4 +4 0 +6
Et si la taille de l'image n'est pas un multiple de 8 ? On la complète de la manière la plus naturelle possible afin de minimiser les hautes fréquence et ainsi augmenter le taux de compression en diminuant la visibilité des artfefacts. Par exemple en utilisant les fonctions de prédiction.
Pour l'encodage le décodage des fichiers JPEG, cherchez sur le web : « Understanding and Decoding a JPEG Image using Python »
MPEG
La compression MPEG (Moving Picture Expert Group) permet de comprimer de la vidéo en tenant compte d'un facteur de qualité afin de produire un débit constant.
MPEG1 : Le but est de pouvoir lire une séquence vidéo et afficher de la vidéo avec un lecteur de CD classique (1.5 Mbit par seconde).
MPEG2 : Le but est de pouvoir coder de la télévision en résolvant le problème de l'entrelacement. Parmi les ajouts:
- Des canaux en plusieurs langues ou surround (5).
- Sous titres
De 3 à 10 Mbit par seconde.
MPEG3 : Extension de MPEG pour la télévision haute définition. En fait cela fixe seulement quelques paramètres, aucun changement d'algorithme.
MPEG4 : Compression de données multimédia pour diffusion avec une bande passante très faible.
- Idées principales:
- Un dialogue entre le compresseur/décompresseur pour déterminer leurs possibilités respectives.
- Un LANGAGE extensible de communication.
- Le MPEG3 comme outil de base
- Delivery Multimedia Integration Framework (DMIF) pour la communication.
- Découpage de l'image en zone (quadtree) et couches (image de fond). Algorithmes spécifiques par zone. Utilisation de modèles 3D texturés.
Comme pour JPEG, le standard ne formalise que la manière de décompresser et donne seulement des indices pour la compression.
Pour le son, c'est ce qui a été décrit précédemment.
Les images sont dans l'espace YUV (U=R-Y, V=B-Y). Les images U et V sont classiquement à une résolution réduite car l'oeil est moins précis dans l'espace des couleurs. Les images sont découpées en block de 16x16 dans l'espace des Y.
- Les images (frames) peuvent être Initiales, Prédites, Bidirectionnelle.
- Pour pouvoir faire de l'accéléré, (ou récupérer des erreurs de transmission) il faut coder régulièrement des images I.
- Les images P ne dépendent que de l'image précédente.
- Les images B sont une interpolation entre une image passé et une image futur. Elles ont disparues en MPEG2.
- Quelques cas courants :
- IIIIIIIIIIIII : format MJPEG, c'est une succession d'images initiales. Seulement utilisé par les premiers appareil photo numériques permettant de faire de la vidéo.
- IPPPPPPPPPPPP : compression maximum pour le satellite et l'ADSL le zapping est lent. Les images I sont inserrés au moment des changements de scène
- IBPBIBPBI : augmente la latence et complique la compression.
Un image I ne comporte que des bloc JPEG de type I, une P peut contenir des I et P et une B des I, P et B. Le codage est le même que celui du JPEG mais il y a un code End Of Block pour éviter de coder le dernier nombre de 0.
Un bloc P est la DCT de la différence entre le bloc à compresser et un bloc de l'image précédente décalé par rapport à la position courante. Classiquement la différence est nulle car on retrouve le bloc ailleurs au bruit près. On a donc seulement besoin de coder la translation.
Un bloc B code la différence par rapport à la moyenne de deux blocs, un dans le passé et un dans le futur. Le futur doit donc déjà être transféré. Cela augmente donc la latence.
Le canal est décomposé en 3 sous-canaux (ou plus dans le futur): audio (2-5 sous-canaux), vidéo, système (synchro et autres informations) Le codage est fait de telle manière que cela reste compatible downward et upward. Le codage permet de multiplexer une hiérarchie de canaux.
MPEG1 : Compression du son 6:1, soit 0.25 Mbit/s, reste donc 1.25 Mbits/s pour le reste. L'image fait 352×240×30. Pour la coder, il faut une compression 26:1 (en fait entre 8 et 30)
Télé numérique
Le décodeur reçoit un signal pour une bande de fréquence. Plus la bande est étroite, plus on perd de place entre les bandes, on ne s'amuse donc pas à coder une chaîne par bande.
Le signal permet de coder plusieurs chaînes en parallèle.
Le nombre de chaînes dépend de la qualité voulue.
Statistiquement, le débit nécessaire est constant. Par exemple, pas de changement de plan sur toutes les chaines simultanément.
Compression hiérarchique
Déjà abordé pour le JBIG.
L'ancêtre de la compression par ondelette est basée sur l'utilisation de pyramide Gaussienne et Laplacienne.
Pyramides Gaussienne et Laplacienne.
On choisi une opération permettant de diminuer la résolution d'une image en perdant le moins d'information possible et sans faire apparaître de moirés, donc en filtrant.
Exemples de filtre pour calculer une image avec une résolution deux fois plus faible :
- \(\frac{p_{i-1}}{4} + \frac{2p_{i}}{4} + \frac{p_{i+1}}{4}\)
- \(\frac{p_{i-2}}{16} + \frac{4p_{i-1}}{16} + \frac{6p_{i}}{16} + \frac{4p_{i+1}}{16} + \frac{p_{i+2}}{16}\)
On prend l'opération inverse qui à partir d'une image à faible résolution retrouve l'image à haute résolution. Les coefficients sont les mêmes que pour l'opération précédente.
On transmet la différence, elle a une dynamique plus faible et donc prend moins de place. On applique évidemment l'algorithme de manière récursive sur la Gaussienne :
Image initiale :
9 8 5 4 2 1 1
Gaussienne, la résolution est divisée par 2 :
7.5 3.75 1.25
Laplacienne calculée à partir de la Gaussienne :
7.5 6.5625 3.75 3.125 1.25 1.25 1.25
Erreur commise, c'est ce que l'on transmet :
1.5 1.4375 1.25 0.875 0.75 -0.25 -0.25
On applique le même coefficient de qualité que pour le JPEG. Le facteur diviseur est le même pour tous les pixels d'un niveau de la pyramide car la fréquence du signal est la même sur le niveau entier.
Ondelette
La version précédente transmet l'image à résolution initiale pour le bas niveau, mais ce n'est pas la peine.
La version présentée est la version la plus simple des ondelettes que l'on puisse faire (ondelettes de Haar)
Au lieu de calculer les différences avec une image agrandie, on calcule la différence avec la moyenne. On a donc (A+B)/2 et (A-B)/2 et donc on peut retrouver A et B. Comme on calcule la différence au niveau du dessus, on stocke deux fois moins de différences, on peut même calculer l'ondelette sur place. De plus, on ne se pose pas de question sur la manière de faire l'agrandissement :
| Image | a | b | c | d | e | f | g | h |
| Etape 1 | (a+b)/2 | (a-b)/2 | (c+d)/2 | (c-d)/2 | (e+f)/2 | (e-f)/2 | (g+h)/2 | (g-h)/2 |
| A | envoit | B | envoit | C | envoit | D | envoit | |
| Etape 2 | (A+B)/2 | (A-B)/2 | (C+D)/2 | (C-D)/2 | ||||
| X | envoit | Y | envoit | |||||
| Etape 3 | (X+Y)/2 | (X-Y)/2 | ||||||
| envoit | envoit | |||||||
On envoit des basses aux hautes fréquences, il y a autant de valeurs à envoyer que de valeurs initiales si les tailles sont des puissances de 2.
Cette méthode s'applique à toutes les valeurs pour lesquelles calculer une somme et une différence a un sens.
Si l'on utilise une base plus large, les différences sont encore plus petites :
- Somme (A+2B+C)/4 et différence (-A+2B-C)/4
- Somme (A+3B+3C+D)/8 et différence (A-3B+3C-D)/8
- Somme (A+4B+6C+4D+E)/16 et différence (A-4B+6C-4D+E)/16
On reconnait les coefficients du triangle de Pascal.
Image 2D
On applique l'algorithme précédent dans un sens puis dans l'autre. L'ordre horizontal ou vertical ne change pas le résultat du calcul :
Image initiale :
Passage horizontal :
Passage vertical :
Les gros carreaux représentent les plus hautes fréquences et sont transmis en dernier.
Ligne brisée
Il est possible de calculer des ondelettes sur des polygones ou bien des polyèdres. En appliquant la formule habituelle, la moyenne est un point et la différence un vecteur (pour les polygones). On stocke le premier point puis les vecteurs.
Si le codage est bien fait on a une invariance par translation, rotation et homothétie. On code le vecteur par rotation/homothétie par rapport au vecteur du niveau au dessus. On a donc à coder des suites des vecteurs très peu différents les uns des autres.
OPUS Audio Codec
Il est garanti que ceci contient des erreurs, comprendre cette méthode dans le détail nécessite des semaines de travail.
Le RFC en cours de rédaction (160 pages sans les sources) contient les sources du codeur et décodeur. Les sources fournis permettent de lever les ambiguïtés qui pourraient être présentes dans le texte anglais.
Intro
Deux méthodes de compressions différentes, une pour les hautes fréquences (la musique) et une pour les basses fréquences (la voix).
Adapté à l'intéractivité : encode frames of 2.5, 5, 10, 20, 40 or 60 ms
Le flux de donnée encode aussi les changements de paramétrage de l'encodage.
Bande passante : de 6kb/s à 510kb/s (cela n'a pas de sens d'avoir une bande passante plus grande car il suffit d'employer un codec sans perte).
Réglage possible de la dépendance des frames entre elles. S'il n'y a pas de codage relatif on est tolérant aux pertes de packets. Les frames dans le même paquet utilisent obligatoirement la redondance.
Forward error correction (FEC) : Le paquets audio contenant des informations importantes sont envoyés une deuxième fois avec une mauvaise qualité au cas ou le premier paquet est été perdu.
Discontinuous transmission (DTX) : moins de paquets envoyés pendant les silences.
Extensible : si un paquet n'est pas conforme au standard, il doit complètement être ignoré. Ceci est détectable car il y a un peu de redondance.
En interne les calculs sont faits à 48kHz même quand le signal à traité fait du 4kHz. Ceci permet de simplifier le code.
Encodage
Entête
Il est fait par paquet (le but est de transmettre sur le réseau).
Le premier octet contient :
- Le type d'encodage du paquet (32 différents)
- Le nombre de frames dans le paquet (1, 2 ou variable)
- Si c'est stéréo.
Les deux encodeurs sont SILK (Modèle de voix) et CELT (MDCT). SILK contient des milliers de valeurs précalculées et modélise le son à reproduire. Les coefficents du modèle sont prédits et les coefficients de la prédiction sont associés à des probabilités. Les blocs de la MDCT se chevauchent. Le traitement est fait de telle manière que le signal est ajusté en fonction de la distance au centre.
S'il y a plusieurs frames dans le paquet, il est nécessaire d'encoder leurs longueurs :
- 0: No frame (discontinuous transmission (DTX) or lost packet)
- 1...251: Length of the frame in bytes
- 252...255: A second byte is needed. The total length is (len[1]*4)+len[0]
DCT
Les bandes de fréquences sont perceptuelles et donc de taille logarithmique. L'énergie transportée par chaque bande est codée à part. La voix est compréhensible en transmettant seulement cette énergie.
Pour coder la DCT de la bande on lui soustrait l'énergie moyenne puis on sélectionne les pics les plus importants pour définir un entier. On fait donc dans la quantification. La taille de cet entier est prédéfinie par le nombre de bits de codage.
Comme les DCT sont sur des bandes petites, les fréquences calculées sont imprécises. Cette suite d'opération est affinée en précalculant des fréquences présentes dans un signal plus long et non sur quelques enchantillons.
Équilibrage des probabilités (entropy coder)
Ils utilisent un range encoding (1976) qui est la même chose que le codage arithmétique mais fonctionne sur des entiers au lieu de réel. Cette manière de procéder est plus rapide.
Leur version de range encoding reporte toutes les erreurs d'arrondi sur le 0 pour augmenter sa probabilité et donc diminuer sa place.
Compression fractale
Très complexe et peu utilisée actuellement car le temps de compression est trop important.
L'idée est de reconstruire un modèle fractale à partir de l'image ou de parties de l'image. On utilise un modèle fractal car les images sont couramment auto-similaires.
Les modèles utilisés sont souvent basés sur les IFS (Iterated Function Set). Un modèle IFS est défini par un ensemble de transformations \(T\) contractantes qui appliquées de nombreuses fois tendent vers le même objet. L'objet est défini de manière récursive.
Le fameux triangle de Sierpińsky :
Pour l'adapter à la compression d'image une transformation est couramment définie par :
- Rectangle de départ dans l'image
- Rectangle d'arrivé (plus petit que le rectangle de départ)
- Une valeur de correction de contraste entre 0 et 1 (qui multiplie la valeur du pixel calculé)
- Une valeur de correction de luminosité (qui s'additionne à la valeur calculée)
Remarques :
- L'image compressée est codée par l'ensemble des transformations.
- L'exécution d'une transformation prend le rectangle initiale, le réduit, corrige le contraste et la luminosité et stocke le résultat dans le rectangle final.
- Décompression de l'image :
- On initialise l'image avec n'importe quoi.
- On itère les transformations jusqu'à ce que l'image soit stable (ça marche car les transformations sont contractantes)
- L'ensemble des rectangles d'arrivé doit recouvrir la surface de l'image.
- L'image reconstruite peut être à n'importe quelle résolution.
- La compression est complexe car l'on doit trouver la transformation qui produit le rectangle final le plus ressemblant au rectangle original.
Compression vidéo par cellule
Utilisé pour les vidéoconférences. L'intérêt est que le taux de compression est constant et que la compression est rapide.
Pour l'ensemble de l'image on extrait une palette de 256 couleurs les plus utiles. On est pas forcé de le faire à chaque image.
- Pour chaque cellule (groupe de 4×4 pixels, donc 48 octets)
- On calcule la moyenne de la luminosité
- On bipartitionne en fonction de la moyenne (on stocke 4×4 bits : 2 octets)
- On calcule les deux moyennes de couleurs des 2 zones
- On stocke les 2 couleurs moyennes (on stocke 2 index de 8 bits : 2 octets)
Taux de compression fixe de 12.
- Les implémentations sont multiples, les extensions sont nombreuses :
- On utilise Huffman pour stocker les événements bitmap et moyennes
- On stocke la différence par rapport à une cellule de l'image déjà calculée.
- On change la palette de couleur pour l'améliorer peu à peu.
La difficulté est d'avoir un catalogue permettant une recherche rapide de l'image la plus ressemblante.
Vidéo conférence
Utilise cette compression ou les normes CCITT qui font aussi de la DCT.
- (CCITT) H.261 : Super CIF (704x576 pixels) format or CIF (352x288 pixels) format or QCIF (176x144 pixels).
- (CCITT) H.263
Correction d'erreur
On ne peut pas attendre de corriger une erreur pour afficher l'image. Donc s'il y a eu une erreur de transmission, il faut continuer à afficher même si c'est faux.
Pour rattraper le coups, il faut que le compresseur envoie une donnée initiale pour que le décompresseur corrige l'erreur. Pour ce faire, le compresseur indique la liste des paquets reçus sans erreur.
Ceci ne peut pas être fait quand on fait du multicast à de très nombreux participants.
Codage et Compression de polyèdre
Beaucoup de chose sur la compression des coordonnées et de la connectivité. C'est un sujet toujours d'actualité.
- Idées en vrac :
- Ne considérer que les triangles.
- Coordonnées relatives à la précédente dans des unités liées à l'objet : Coder des vecteurs au lieu de positions.
- On quantifie les vecteurs qui sont normalement petits.
- Ne jamais transmettre 2* le même point.
- Problème du codage de la normale à une surface (échantillonnage régulier de la surface de la sphère).
- Simplification inversible : on fourni une donnée minimum pour rajouter les facettes enlevées (même idée : on transmet le son milieu, puis le son gauche, ou bien les turbo code).
- Pour la topologie : arbres de triangles (2.2 bits par triangle en moyenne) ou bien le parcour du polyèdre en spiral si c'est possible.
- Pour la transmission simplifiée : enlève les facettes presque coplanaires.
- Utiliser des méthodes multirésolution, ondelettes par exemple.
Les polyèdres sans trou peuvent être représentés par des cartes planaires, c'est-à-dire un graphe sans croisement.
Méthode de la spirale
Pour chaque facette, un bit indiquant si l'on ajoute un point ou pas. Les coordonnées sont en relatifs et avec une faible précision.
Attention, dans certains cas on peut aboutir à des impossibilités : réutiliser un point existant sans réutiliser l'arête existante. Ces cas se produisent quand on termine le polyèdre et que la partie extérieure de l'enveloppe se touche elle-même.
- Solutions :
- Modifier le polyèdre pour que ce cas ne puisse pas se produire.
- Faire plusieurs sous polyèdres.
- Augmenter la taille du langage pour le codage, mais cela pénalise tout le monde.
Mots planaires
Méthode générale de codage des polyèdres quelconques dans un espace de dimension quelconque. Cela code les même choses que les N-G-Cartes mais de manière efficace. Le parcours d'un mot planaire permet d'afficher le polyèdre directement en ne faisant chaque calcul et affichage qu'une unique fois.
Soit la carte planaire décrivant le cube et son mot planaire :
Formats de fichiers
Ils permettent d'expliquer ce qu'ils contiennent.
PNM
Utilitaires du package netpbm
Portable N.={Bit, Gray, Pixel} Map
L'entête pour les fichiers RAW (pas codé en décimal mais en binaire) :
- PGM RAW : P5\n%d %d\n%d\n avec la largeur en pixel, la hauteur en pixel, une valeur indiquant le nombre de bits par pixels qui est systématiquement 255.
- PBM RAW : Idem avec P4 et 1 bit par pixel
- PPM RAW : Idem avec P6 et 3 octets par pixel
Dans les 3 cas l'image est une suite de valeurs binaires non lisibles par un être humain.
La deuxième ligne peut être un commentaire, elle commence alors par #
Conversion d'image :
Avec les outils netpbm on fait un pipeline avec des commandes Xtop[bgpn]m | p[bgpn]mtop[bgpn]m | p[bgpn]mtoY
Avec la commande convert de imagemagick : convert toto.X toto.Y
En langage C, pour écrire directement une image JPG sans stocker une image non compressée sur le disque :
FILE * f = popen("ppmtojpeg >toto.jpg", "w") ; fwrite(votre image en PPM) ; pclose(f) ;
TIFF
La référence : http://partners.adobe.com/public/developer/en/tiff/TIFF6.pdf
TIFF est un format extensible pour stocker n'importe quoi, il a servi de base à beaucoup d'autres formats. Il est néanmoins limité à des fichiers de 4Go.
Entête
Un offset est un pointeur à l'intérieur du fichier (ou du flux).
Les mots sont de 16 bits.
- Mot 1 : (4949) ou (4D4D) Little ou Big endian pour 16 ou 32 bits.
- Mot 2 : (2A)
- Mot 3→4 : (XXXXXXXX) offset premier IFD dans le fichier
IFD (Image File Directory)
Il y en a un par image
- Mot 1 : (XXXX) Nombre d'entrées dans l'IFD
- Mot 2→n-1: Les entrées
- Mot n→n+1 : (XXXXXXXX) Offset IFD suivant ou 0 pour le dernier
Directory
- Mot 1: Tag
- Mot 2: Type (1:octet non-signé, 2:ASCII-7bit, 3:Short, 4:Long, 5:Rationnel...
- Mot 3→4: nombre d'élément (chaîne de caractères ou tableau)
- Mot 5→6: Offset sur la valeur (ou la valeur elle même si elle tient sur moins de 4 octets)
Quelques Tag possible parmis la centaines existant :
- 100 Largeur de l'image
- 101 Hauteur de l'image (nombre de lignes)
- 102 Bit par échantillon (par pixel ou bien dans colormap) fois 3 si RVB
- 103 1: pas de compression, 2: CCITT groupe 3, 6: JPEG
- 106 0: White is zero, 1: Black is zero, 2: RGB, 3: Palette
- 111 StripOffset On est pas forcé de transmettre et d'afficher l'image linéairement, on peut transmettre les bandes paires puis les bandes impaires.
- 115 1: gris, 3: couleur
- 116 RowPerStrip La compression est faite dans les strips.
- 117 StripByteCount
- 11A Pixel par unité suivant X
- 11B Pixel par unité suivant Y
- 128 ResolutionUnit 1: non, 2: inch, 3: centimètre
- 140 Le pointeur sur colormap
Et en plus: Artist, Date, Host, Image, Description, Make, Model, Software, WhitePoint, données pour le JPEG, ...
AVI
Un FOURCC est un code sur 4 octets créé par la concaténation de 4 caractères, ils sont lisibles par les êtres humains. Seulement 3 entités différentes :
- Entête : 'RIFF' fileSize fileType
- Une liste : 'LIST' listSize listType listData
- Un bloc de données (chunk) : FOURCC ckSize ckData
Le décompresseur peut analyser le fichier AVI sans rien savoir d'autre. Mais il ne comprendra pas les FOURCC définissant les blocs audio, vidéo...
Si l'on plonge en plein milieu d'un fichier il n'est pas très difficile de retrouver un endroit ou commencer à décoder.
EXIF
C'est un ensemble de TAG normalisés compatible TIFF que l'on peut insérer dans presque tous les formats de fichier.
La manière de l'insérer dépend malheureusement du format du fichier.
Portable Network Graphic
En vrac :
- Palette ou true-color.
- Meilleur compresseur que GIF.
- Code correcteur d'erreur : CRC
- Transparence paramétrable.
- Extensible.
- Gamma.
- Affichage progressif (gris puis couleur, général puis détails).
- Coordonnées XY (CIE 1931) du RVB et blanc.
- Données textuelles.
VRML et X3D
VRML 1.0 is a subset of the Inventor File Format (ASCII) with some additions to allow linking out to the Web and including other URLs. The linking out feature (WWWAnchor) provides the same feature that HREF anchors provide in HTML.
Just before the VRML press announcement, Mark described VRML in a "backgrounder" (URL is http://vrml.wired.com/arch/1010.html) " VRML is a language for describing multi- user interactive simulations -- virtual worlds networked via the global Internet and hyperlinked within the World Wide Web."
VRML 1.0
Le format est un texte lisible avec une syntaxe simple. Ce texte est verbeux Translation et pas Tr. mais une fois comprimé, cela change peu la taille finale.
- Arbre de primitives, d'attributs, de liens WWW, d'inline VRML
- Très proche de GL pour la richesse de définition du modèle en terme d'attributs graphiques.
- Des objets de bases simples.
- Seul des unions car cela n'est pas volumique.
- Des accélérations graphiques basées sur la visibilité.
- La complexité du modèle dépend de la distance (LOD : Level Of Details)
- Cliquer sur un objets permet de suivre un lien vers d'autres objets (HTML ou VRML)
VRML la suite
Elle nécessite un langage interprété. Peut-être du JAVA-VRML?
- behaviors (objects behave based on time and events)
- interactions (a way to feed events into environments)
- multiple participants
- sound (if it was not in VRML 1.1)
- telepresence
- compression : la version binaire est intégré avec compression des modèles facette dans MPEG-4 en 1998.
Exemple
#VRML V1.0 ascii
Separator {
DirectionalLight {
direction 0 0 -1 # Light shining from viewer into scene
}
PerspectiveCamera {
position -8.6 2.1 5.6
orientation -0.1352 -0.9831 -0.1233 1.1417
focalDistance 10.84
}
Separator { # The red sphere
Material {
diffuseColor 1 0 0 # Red
}
Translation { translation 3 0 1 }
Sphere { radius 2.3 }
}
Separator { # The blue cube
Material {
diffuseColor 0 0 1 # Blue
}
Transform {
translation -2.4 .2 1
rotation 0 1 1 .9
}
Cube {}
}
}
X3D
La version VRML en XML qui est intégrable directement dans le HTML.
Mais tout ceci semble mort car il est plus simple et performant de tout recoder soit même en WebGL car créer de nombreux objets 3D dans le DOM n'est pas utilisable pour des problèmes réels.
WML (utilisé par WAP)
WAP Wireless Application Protocol permet de diffuser des pages web sur des périphériques peu puissant.
WML est un XHTML simplifié.
WBXML WAP Binary XML Content Format permet d'encoder efficacement le XHTML.
Les éléments sont codés par un octet contenant :
- 1 bit indiquant s'il contient une liste d'attributs
- 1 bit indiquant s'il contient des fils
- 6 bits pour le numéro du TAG ou LITERAL pour l'indiquer en texte ou END pour terminer la liste des éléments.
Les attributs sont codés par :
- Un octet <128 indiquant le numéro d'attribut ou LITERAL pour l'indiquer en texte ou END pour terminer la liste des attributs.
- Une suite d'octets >128 représentant des chaines de caractères qui sont concaténées pour obtenir la valeur de l'attribut. Ou bien un litéral.
Divers
Stéganographie
La stéganographie est l'écriture cachée. En clair, l'art de cacher une information dans une autre information. Cette technique suscite de nombreuses recherches car elle permet par exemple de stocker une information (un copyright) dans des données sans que celle-ci soit enlevable sans beaucoup abimer les données.
Exemple venant de : Neil F. Johnson, Steganography, Technical Report TR_95_11_nfj, 1995. http://www.jjtc.com/pub/tr_95_11_nfj/
News Eight Weather: Tonight increasing snow. Unexpected precipitation smothers eastern towns. Be extremely cautious and use snowtires especially heading east. The highways are knowingly slippery. Highway evacuation is suspected. Police report emergency situations in downtown ending near Tuesday.
En prenant la première lettre de chaque mot : Newt is upset because he thinks he is President
Pendant la seconde guerre mondiale, certain services secrets réécrivaient les correspondances pour éviter des transferts d'information par ces méthodes.
Dans le cadre d'une implémentation informatique (pas de standards pour le moments), 3 méthodes peuvent être cataloguées :
- Stéganographie simple : on extrait le message de la donnée. Cette méthode n'est pas fiable si l'agorithme est connu, on ajoute donc une graine qui définie la position de l'information.
- Filigrane (WaterMarking) : on extrait le message de la donnée et de la donnée initiale, le message est perdu si la donnée initiale l'est.
- Empreinte digitale (FingerPrint) : le message étant donné on regarde si on le retrouve dans la donnée.
Méthode simple pour les sons et images : on modifie des bits de poids faibles de la donnée. On peut enlever le marquage à condition de modifier tous les bits de poids faibles. L'inconvénient de cette méthode est quelle ne résiste pas à la DCT avec perte ou à des pertes de qualité d'image.
Méthode utilisant la DCT : on code le message dans les bits de poids faible des coefficients de la DCT après quantification. Cette méthode est plus résistante mais le message disparaît si l'on compresse avec une qualité moins bonne.
Compression entêtes TCPIP
La norme est définie dans le RFC1144
C'est pour les liaisons bipoint faible début (liaisons séries par exemple). Il faut qu'au 2 bouts le protocole compressé soit supporté.
L'implémentation de la méthode de compression fait 250 lignes de C 90 micro secondes sur un 68020 a 20MHz pour compresser l'entête.
Un header TCPIP classique occupe 20 octet pour IP et 20 octets pour TCP. Le header après compression se réduit à 3 octets.
Tout d'abord, les paquets venant d'une même connexion ont très peu de champs qui changent. Le codage va donc s'appuyer sur cela :
- Bit 1 : indique si c'est compressé.
- Nombre : Numéro session TCP - Numéro session TCP paquet précédent.
- Un mask de bits indiquant les champs variants dans le header TCPIP
- Pour chaque champs variant on stocke la différence par rapport à la valeur du paquet précédent de la même connexion.
Les nombres sont codés sur un nombre de bits variables (comme dans la DCT) si une des valeurs change de plus de 65536. On envoit un paquet non compressé.
On envoit en plus un CRC sur le paquet compressé, car des erreurs de transmission sur le paquet compressé ont tendance à générer des paquets TCPIP décompressés valides !
Si les 2 codes d'erreur ne détectent rien, une erreur passe à travers. Les paquets suivants ne vont pas passer car invalides. Dans ce cas, il n'y a pas de transmission d'acquittement. Au bout d'un timeout, la retransmission est faite avec un paquet non-compressé afin de reprendre proprement.
Cette compression fonctionne bien mieux qu'une compression LZW aveugle.
Il est plus intéressant de compresser séparement l'entête et les données. On peut activer dans les serveurs web une compression automatique des données transmises (pas des entêtes).
Utilisé par PPP
PPP (Point-To-Point Protocol) s'appuis sur les normes de transmission ISO 3309, 4335 et 6256. Tout comme X.25.
On peut faire du PPP a travers n'importe quel couche de transmission, liaison série, parrallèle, X.25 (RFC 1598)... malheureusement ils ne peuvent pas partager un même lien physique, il faut encapsuler PPP. L'encapsulation n'est pas totale car la couche X.25 garantie déjà beaucoup sur la transmission, pas la peine de refaire les mêmes tests 2 fois.
Lors de l'établissement de la liaison PPP on négocie si les entêtes IP seront compressées.
Utilisé par SLIP (CSLIP)
Serial Line IP (RFC 1055).
Son nom indique la différence.
Les performances sont les mêmes.
SLIP n'a pas été normalisé.
Il est en voie de disparition.
Anomalies
La compression peut être utile pour trouver des données anormales dans un ensemble de données. En effet, une donnée anormale se comprime moins bien qu'une donnée normale.
Application aux fichiers tabulés (fichier de log par exemple). On évalue le nombre d'informations pour stocker une ligne. Le principe est simple :
- On initialise la quantité d'information de chaque ligne à 0
- On recherche la colonne contenant le plus de caractères identiques. On bipartitionne alors l'ensemble des lignes.
- Pour les lignes contenant ce caractère dans cette colonne on incrémente la quantité d'information de 1/nbLignes puisque le caractère est codé une seule fois pour toutes ces lignes. On enlève la colonne et on continue la récursion sur ces lignes.
- Celles ne le contenant pas, on ne fait rien et on continue la récursion.
Une ligne complètement différente des autres se trouvera rapidement seule et la récursion se poursuivra à gauche en ajoutant systématiquement 1 à sa quantité d'information.
100 lignes identiques prendront 100 fois moins de mémoire.
Cette méthode permet de trouver toutes les anomalies dans les fichiers de log. Il convient d'intégré progressivement les informations dans les fichiers de log servant de dictionnaire afin qu'un pirate ne submerge les fichiers de log avec de nombreuses anomalies identiques.
Base de données
Les BD utilisent la compression comme critère de normalisation. En effet, dans un bon schéma de base de donnée aucune donnée n'est dupliquée. Cela a de nombreux avantages :
- Cela prend moins de place (mais lent si l'on ne crée pas les bonnes vues)
- Il ne peux pas y avoir d'incohérence.
- Cela force à structurer correctement la base de donnée.
Programmation
Voir la première partie de http://perso.univ-lyon1.fr/thierry.excoffier/COURS/COURS/TRANS_COMP_IMAGE/prog.html