M2 - Images


TP1 - transformations et pipeline



 

Partie 1 : affichage d'une primitive.


L'opération fondamentale réalisée par un pipeline de rendu est le dessin d'une primitive : déterminer quels pixels permettent de remplir une forme "simple" dans l'image résultat.

Cette opération est découpée en plusieurs étapes :


exercice 1 : transformations

    Les objets et leurs sommets sont décrits dans un repère local, puis ces objets sont placés et orientés dans le repère de la scène. Un observateur / camera est également placé et orienté dans le repère de la scène. Une transformation de projection 3d vers 2d est aussi associée à l'observateur. Ces 3 transformations sont classiquement représentées par des matrices homogenes 4x4 :
    Model (transformation du repère local au repère de la scène),
    View (transformation du repère de la scène au repère camera)
    Projection (transformation du repère camera au repère projectif homogène de la camera).

Plus une autre qui représente les dimensions de l'image résultat :
    Viewport (transformation du repère projectif homogène vers le repère de l'image).

Il est possible de composer ces matrices afin de construire une seule matrice de transformation permettant de passer directement du repère local de l'objet au repère de l'image. Ecrivez cette relation.

Par construction de la transformation de projection, les points visibles par l'observateur se retrouvent dans le repere projectif (après transformation) à l'interieur du cube unitaire [-1 1] sur les 3 axes.

Si l'on choisit une matrice identité comme projection, ou peut on placer des points qui seront visibles / associés à un pixel de l'image ?



prise en main de gKit :

installez gKit et ses dépendances.

compilez la doc avec Doxygen.
Elle sera consultable dans doc/html/index.html. Les classes de bases sont documentées dans la partie module de la documentation générée.

gKit utilise la classe gk::Transform pour représenter et manipuler les transformations. Les classes gk::Point et gk::Vector permettent de représenter un point et un vecteur. Les fonctions de construction des transformations standards sont aussi disponibles : gk::Translate(), gk::Rotate(), gk::Perspective().

La transformation d'un point s'écrit directement :
    gk::Transform T;      // identité
    gk::Transform T= gk::RotateX(30);    // rotation de 30° autour de l'axe X
    gk::Transform T= gk::Translate( gk::Vector(0, 0, 50) )    // translation sur l'axe Z

     gk::Point p;
    gk::Point q= T(p);    // renvoie le point reel transforme

La composition de transformations est aussi disponible :
    gk::Transform A, B;
    gk::Transform C= A * B;

La transformation inverse est également calculée :
    gk::Transform M= C.inverse();

Pour obtenir le point homogène après la transformation d'un point p :
    gk::HPoint h;
    M(p, h);    // renvoie le point homogene apres la transformation

Si le point homogène est dans la zone visible (le cube unitaire -1, 1), on peut le projetter / normaliser pour obtenir le point 3d associé :
    gk::Point q;
    if(h.isVisible())
        q= h.project();    // projette le point homogene dans l'espace 3d reel.


gKit utilise la classe gk::Image pour représenter un ensemble de pixels et fournit également des fonctions permettant d'enregistrer l'image dans un fichier.
gk::Image *image= new gk::Image(largeur, hauteur);
gk::ImageIO::writeImage("resultat.bmp", image);

Les méthodes gk::Image::pixel(x, y) et gk::Image::setPixel(x, y, color) permettent de lire et de modifier la couleur du pixel de coordonnées x, y.
La classe de base gk::Color représente une couleur par comme un vecteur à 4 composantes : rouge, vert, bleu, transparence.

exemple:

#include "Vec.h"      // type vecteur, point, couleur, etc. de "base"
#include "Image.h"    // classe image
#include "ImageIO.h"  // entrees / sorties sur des images

int main( )
{
    gk::Image *image= gk::createImage(512, 512);    // cree une image de 512x512 pixels
   
    // parcourir tous les pixels de l'image
    for(int y= 0; y < image->height; y++)    // chaque ligne
        for(int x= 0; x < image->width; x++)    // chaque colonne
            image->setPixel(x, y, gk::Vec4(1, 0, 0, 1));    // colorie chaque pixel en rouge opaque
   
    // enregistre le resultat
    gk::ImageIO::writeImage("out.bmp", image);
   
    delete image;
    return 0;
}

exercice 2 : version fragmentation / rasterization 2D.

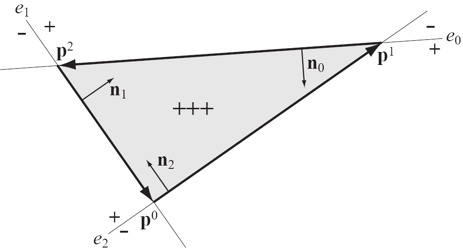
Soit 3 sommets p0, p1, et p2 dans le plan image.



Définissez les équations 2d des 3 arêtes e0, e1, e2, du triangle p0p1p2 sous la forme : e(x,y)= ax + by + c.

Un pixel (px, py) est à l'intérieur du triangle s'il se trouve dans le demi plan positif défini par (la droite portant) chaque arête, c'est dire si e0(px, py) > 0, e1(px, py) > 0 et e2(px, py) > 0.

Comment construire les équations des arêtes pour vérifier cette condition ?
indication :
    l'aire signée d'un triangle orienté dans le plan se calcule directement : cf Modern triangles / section Modern triangles
        pour le triangle p0, p1, p2= 0.5 * [ (x1 - x0) * (y2 - y0) - (x2 - x0) (y1 - y0) ]

    on peut également calculer l'aire signée du triangle formé par l'arete p0p1 et un point p (px, py) du plan image :
        aire p0p1p = 0.5 * [ (x1 - x0) * (py - y0) - (px - x0) (y1 - y0) ]
        e0(px, py) = a0*px + b0*py + c0= [-(y1 - y0)] * px + [(x1 - x0)] * py + [x0 * (y1 - y0) - y0 * (x1 - x0)]

première solution :
    testez tous les pixels du plan image.


solution efficace ?
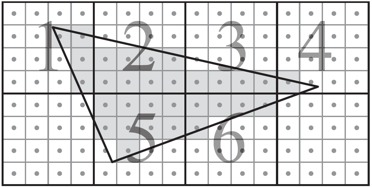
 Proposez une solution qui teste des blocs de pixels dans un premier temps, puis qui teste tous les pixels des blocs couvrant (partiellement ou entièrement) le triangle.




Comment déterminer efficacement qu'un bloc se trouve entièrement à l'extérieur du triangle (sans tester tous les pixels) ?
(indication : ses 4 sommets sont à l'exterieur de la même arête du triangle)

Lorsqu'un bloc contient, au moins partiellement, le triangle, testez tous les pixels du bloc (les blocs 1 à 6 dans l'exemple).

Cette "optimisation" est-elle interressante dans tous les cas ? Comment choisir la taille des blocs ?


question bonus : et en 3D ?
on peut écrire exactement le même algorithme en 3D, en utilisant des tetrahedres et leur volume signé, au lieu d'utiliser l'aire signée de triangles : cf 3D triple product.


pour les curieux : et en 4D ?
Une solution élégante est présentée section 2 dans :
"Incremental and Hierarchical Hilbert Order Edge Equation Polygon Rasterization"
M.D. McCool, C. Wales, K. Moule,
gh 2001


exercice 3 : version Reyes, subdivision.

Une autre solution, applique le principe algorithmique "diviser pour règner" au problème. Il est immédiat de dessiner un objet plus petit qu'un pixel, dans les autres cas, il faut le découper.

Proposez une solution utilisant cette idée.
indication : pour subdiviser un triangle en 4, une solution consiste à calculer le point milieu de chaque arête et à construire les 4 sous triangles.

Cette solution peut-elle fonctionner lorsque certains sommets sont en dehors de la zone visible ? Modifiez votre programme pour inclure cette fonctionnalité.
indication : il serait judicieux d'arreter la subdivision lorsque une partie de la surface est entierement non visible.


exercice 4 : version lancer de rayon.

La dernière catégorie de solution consiste à déterminer l'équation de la droite passant par le centre de chaque pixel de l'image et à tester l'intersection de cette droite avec le triangle.
La classe gk::Triangle fournit le test d'intersection d'un triangle et d'un rayon, cf gk::Triangle::intersect().

Comment calculer les extrémites du rayon passant par le centre du pixel (x, y) ? Dans quel espace est-il le plus simple de travailler ?

indication : la classe gk::Ray représente un rayon par son origine, o,  et sa direction, d. Un point le long du rayon est represente p(t)= o + t . d



Partie 2 : plusieurs primitives

Lorsque la scène est composée de plusieurs objets, il est (très) fréquent que plusieurs triangles recouvrent le même pixel. En général, on souhaite donner au pixel la couleur de l'objet (opaque) le plus proche de la camera.

Comment déterminer la distance associée à un fragment issu d'un triangle ? Comment conserver le plus proche de la camera ?
rappel : la somme des aires des triangles pp0p1, pp1p2, pp2p0 correspond à l'aire de p0p1p2.

Comment réaliser ce test dans la version fragmentation et dans la version Reyes ?
(pourquoi est-ce inutile dans la version lancer de rayons ?)

question bonus : en plus de reconstruire la distance à la camera, on peut appliquer la même démarche à d'autres valeurs associées aux sommets des triangles.